题目内容
已知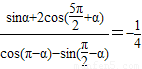 .
.(1)求tanα的值;
(2)求(sinα+cosα)2的值.
【答案】分析:(1)首先应用诱导公式整理所给的函数式,得到一个分子和分母都是一次式的形式,分子和分母同除以角的余弦,得到关于正切的方程,得到结果.
(2)根据同角的三角函数之间的关系,把正弦与余弦的积表示成正切和余切的形式,根据上一问做出的正切的结果,整理出要求的代数式的值.
解答:解:(1)由已知 ,
,
所以 .
.
(2)因为 ,所以
,所以 ,
,
所以 .
.
点评:本题考查同角的三角函数之间的关系及诱导公式的应用,本题解题的关键是整理出正切值,熟练应用同角之间的三角函数的关系,本题是一个基础题.
(2)根据同角的三角函数之间的关系,把正弦与余弦的积表示成正切和余切的形式,根据上一问做出的正切的结果,整理出要求的代数式的值.
解答:解:(1)由已知
 ,
,所以
 .
.(2)因为
 ,所以
,所以 ,
,所以
 .
.点评:本题考查同角的三角函数之间的关系及诱导公式的应用,本题解题的关键是整理出正切值,熟练应用同角之间的三角函数的关系,本题是一个基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
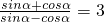 (1)求tanα;(2)求sinαcosα
(1)求tanα;(2)求sinαcosα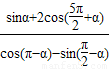 =-
=- .
. ,求β.
,求β. .
. 的值.
的值.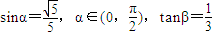 .
.