题目内容
已知2x≤16且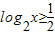 ,
,(1)求x的取值范围;
(2)求函数
 的最大值和最小值.
的最大值和最小值.
【答案】分析:(1)分别利用指数、对数函数的单调性即可求得x的范围,再取交集即可;
(2)根据对数运算性质对f(x)进行化简,然后转化为关于log2x的二次函数,利用二次函数的性质可得函数的最值,注意x的范围;
解答:解:(1)因为2x≤16=24,所以x≤4;
又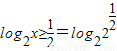 ,所以
,所以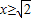 ,
,
故所求x的取值范围是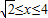 ;
;
(2)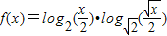 =
=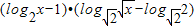
=(log2x-1)•(log2x-2)=
=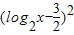 -
- ,
,
由已知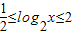 ,
,
所以,当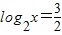 ,即
,即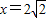 时,f(x)取得最小值
时,f(x)取得最小值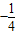 ;
;
当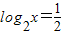 ,即
,即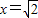 时,f(x)取得最大值
时,f(x)取得最大值 .
.
点评:本题考查对数的运算性质、函数的最值,考查学生的运算求解能力.
(2)根据对数运算性质对f(x)进行化简,然后转化为关于log2x的二次函数,利用二次函数的性质可得函数的最值,注意x的范围;
解答:解:(1)因为2x≤16=24,所以x≤4;
又
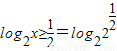 ,所以
,所以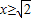 ,
,故所求x的取值范围是
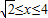 ;
; (2)
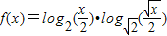 =
=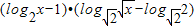
=(log2x-1)•(log2x-2)=

=
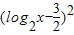 -
- ,
,由已知
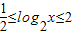 ,
,所以,当
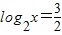 ,即
,即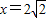 时,f(x)取得最小值
时,f(x)取得最小值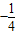 ;
;当
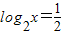 ,即
,即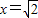 时,f(x)取得最大值
时,f(x)取得最大值 .
.点评:本题考查对数的运算性质、函数的最值,考查学生的运算求解能力.

练习册系列答案
相关题目
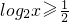 ,
,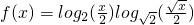 的最大值和最小值.
的最大值和最小值.