Question

如图，设椭圆中心在原点，焦点在x轴上，过椭圆的右焦点F₂作倾斜角为的直线l，交椭圆于M、N两点，已知椭圆的左焦点为F₁，到直线l的距离为,M、N两点到椭圆的右准线的距离之和为,求这个椭圆的方程.

Answer 1

解析：设椭圆方程为=1(a＞b＞0)，直线l与y轴相交于A点，连结F₁A.

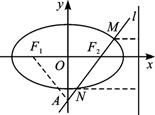
由已知可得△F₁AF₂为等腰直角三角形，且|F₁A|=,

∴|F₁F₂|=2.∴c=1,F₂(1,0).

∴直线l的方程为y=x-1.

设M(x₁,y₁)、N（x₂，y₂），由已知

(-x₁)+(-x₂)=x₁+x₂=-=2a²-.

从而y₁+y₂=(x₁-1)+(x₂-1)=x₁+x₂-2=2a²-.

∵M、N在椭圆上，∴=1,=1,两式相减，得=0 b²(x₁+x₂)+a²(y₁+y₂)·=0.

∴b²(2a²-)+a²(2a²-)=0,

即（a²-1）(2a²-)+a²(2a²-)=0.

∴a²=或a²=2(a²=舍去).

∴b²=a²-1=1.∴椭圆方程为=1.