题目内容
(满分12分)对于函数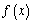 ,若
,若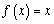 ,则称
,则称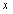 为
为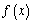 的“不动点”;若
的“不动点”;若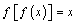 则称
则称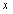 为
为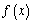 的“稳定点”函数
的“稳定点”函数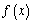 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为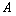 和
和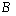 ,即
,即 ,
,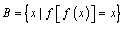 .
.
(Ⅰ) 求证: ;
;
(Ⅱ)若 ,且
,且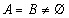 ,求实数
,求实数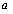 的取值范围.
的取值范围.
【答案】
(Ⅰ)略
(Ⅱ) 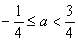
【解析】(1)证明:当 显然成立,
显然成立,
当 时,对
时,对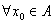 ,有
,有 成立,
成立,
所以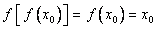 ,即
,即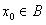 ,所以
,所以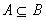 ..............4分
..............4分
(2)由 得
得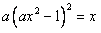 ,即
,即
又因A=B ,所以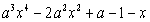 可分解为
可分解为
并且方程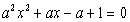 与
与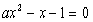 有相同的根或无实根........8分
有相同的根或无实根........8分
当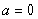 时,
时, ,显然成立,
,显然成立,
当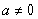 时, 由
时, 由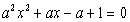 得
得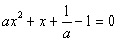 ,显然不可能与方程
,显然不可能与方程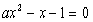 有相同的根,所以
有相同的根,所以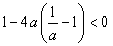 ,解得
,解得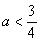
又方程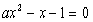 有实根,所以
有实根,所以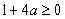 ,解得
,解得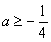
所以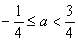 且
且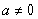
综上所述, 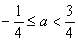 ...........................12分.
...........................12分.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目