题目内容
设集合P={1,a,b},Q={1,a2,b2},已知P=Q,求1+a2+b2的值.
解:∵P=Q,
∴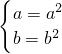 ①
①
或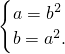 ②
②
解①得a=0或a=1,b=0或b=1.(舍去)
由②得a=b2=a4,∴a=1或a3=1.
a=1不合题意,
∴a3=1(a≠1).
∴a=ω,b=ω2,其中ω=- +
+ i.
i.
故1+a2+b2=1+ω2+ω4=1+ω+ω2=0.
分析:由两个集合相等的条件找出a和b的关系即可.注意集合元素的互异性.
点评:本题考查集合相等、集合元素的性质,属基本题.
∴
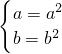 ①
①或
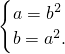 ②
②解①得a=0或a=1,b=0或b=1.(舍去)
由②得a=b2=a4,∴a=1或a3=1.
a=1不合题意,
∴a3=1(a≠1).
∴a=ω,b=ω2,其中ω=-
 +
+ i.
i.故1+a2+b2=1+ω2+ω4=1+ω+ω2=0.
分析:由两个集合相等的条件找出a和b的关系即可.注意集合元素的互异性.
点评:本题考查集合相等、集合元素的性质,属基本题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目