题目内容
(1)△ABC的三边a,b,c倒数成等差数列,求证: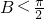
(2)证明: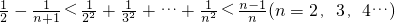 .
.
证明:(1)反证法:假设B≥ .
.
则有b>a>0,b>c>0.
则 ,
,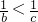
可得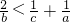 与已知矛盾,
与已知矛盾,
假设不成立,原命题正确.
(2)因为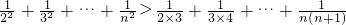
=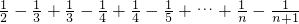
=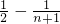 ,
,
所以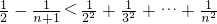 ;
;
下面用数学归纳法证明: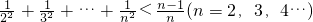 ,
,
①当n=2时,左边=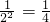 ,右边=
,右边=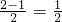 ,左<右,不等式成立.
,左<右,不等式成立.
②假设n=k(k≥2,k∈Z)不等式成立,即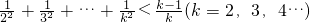 ,
,
那么: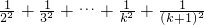
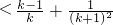 ,
,
要证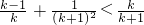 ,
,
只需证明: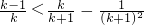 ,
,
即证明: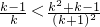 ,
,
就是证明:(k-1)(k+1)2<k(k2+k-1),
只需证明:k3+2k2+k-k2-2k-1<k3+k2-k,
即证明-1<0,这是显然成立的,
所以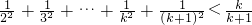 成立.
成立.
这就是说n=k+1时不等式也成立,
由①②可知,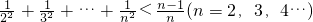 成立.
成立.
综上不等式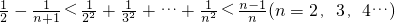 恒成立.
恒成立.
分析:(1)反证法,假设B≥ ,则 b为最大边,有b>a>0,b>c>0.推出与已知矛盾的结果.
,则 b为最大边,有b>a>0,b>c>0.推出与已知矛盾的结果.
(2)利用放缩法以及裂项法求和证明不等式的左侧,右侧不等式利用数学归纳法证明即可.
点评:第一题使用反证法证明,注意反证法的步骤;第二题考查放缩法与数学归纳法证明不等式的基本方法,注意数学归纳法中的分析法的应用,考查分析问题解决问题的能力.
 .
.则有b>a>0,b>c>0.
则
 ,
,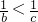
可得
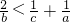 与已知矛盾,
与已知矛盾,假设不成立,原命题正确.
(2)因为
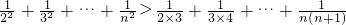
=
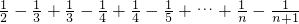
=
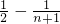 ,
,所以
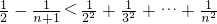 ;
;下面用数学归纳法证明:
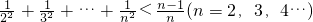 ,
,①当n=2时,左边=
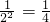 ,右边=
,右边=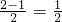 ,左<右,不等式成立.
,左<右,不等式成立.②假设n=k(k≥2,k∈Z)不等式成立,即
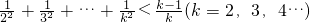 ,
,那么:
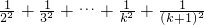
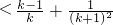 ,
,要证
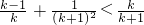 ,
,只需证明:
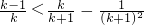 ,
,即证明:
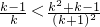 ,
,就是证明:(k-1)(k+1)2<k(k2+k-1),
只需证明:k3+2k2+k-k2-2k-1<k3+k2-k,
即证明-1<0,这是显然成立的,
所以
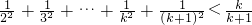 成立.
成立.这就是说n=k+1时不等式也成立,
由①②可知,
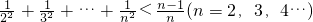 成立.
成立.综上不等式
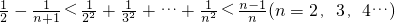 恒成立.
恒成立.分析:(1)反证法,假设B≥
 ,则 b为最大边,有b>a>0,b>c>0.推出与已知矛盾的结果.
,则 b为最大边,有b>a>0,b>c>0.推出与已知矛盾的结果.(2)利用放缩法以及裂项法求和证明不等式的左侧,右侧不等式利用数学归纳法证明即可.
点评:第一题使用反证法证明,注意反证法的步骤;第二题考查放缩法与数学归纳法证明不等式的基本方法,注意数学归纳法中的分析法的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
 (Ⅰ)求直三棱柱ABC-A′B′C′的体积;
(Ⅰ)求直三棱柱ABC-A′B′C′的体积;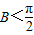
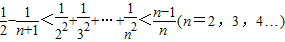 .
.