题目内容
已知函数
(1)求y=f(x)在
 上的单调区间和值域;
上的单调区间和值域;(2)把y=f(x)的图象向右平移
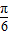 个单位后得到的图象,其大于零的零点从小到大组成数列{xn},求数列{xn}的前n项和Sn.
个单位后得到的图象,其大于零的零点从小到大组成数列{xn},求数列{xn}的前n项和Sn.
【答案】分析:(1)利用二倍角公式与两角和的正弦函数化简y=f(x),利用正弦函数单调增区间和单调减区间,解出函数的单调区间;
(2)通过左加右减的原则求出y=f(x)的图象向右平移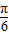 个单位后得到的图象对应的解析式,其大于零的零点从小到大组成数列{xn},然后求解数列{xn}的前n项和Sn
个单位后得到的图象对应的解析式,其大于零的零点从小到大组成数列{xn},然后求解数列{xn}的前n项和Sn
解答:解:(1)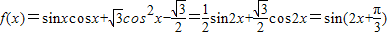 ,
,
当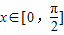 时,
时,
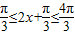 ,
,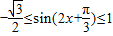 ,
,
故值域为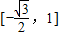 ,
,
令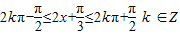 ,解得
,解得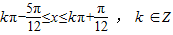 ,
,
k=0时,解得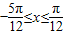 ,又
,又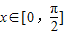
所以当 上函数
上函数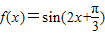 单调递增,
单调递增,
令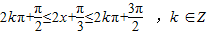 ,解得
,解得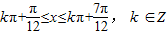 ,
,
k=0时,解得 ,,又
,,又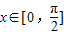
所以当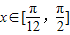 上函数
上函数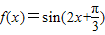 递减
递减
综上,在区间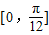 上函数
上函数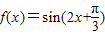 单调递增,在区间
单调递增,在区间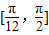 上函数
上函数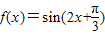 递减.
递减.
(2)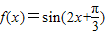 右平移
右平移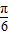 个单位后得到g(x)=sin2x,
个单位后得到g(x)=sin2x,
令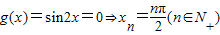 ,数列{xn}是以
,数列{xn}是以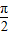 为首项,以
为首项,以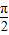 为公差的等差数列
为公差的等差数列
故其前n项和为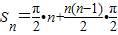 =
=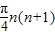 ,
,
点评:本题考查三角函数的化简求值,二倍角公式与两角和的正弦函数的应用,考查函数与数列相结合的问题,考查计算能力.
(2)通过左加右减的原则求出y=f(x)的图象向右平移
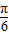 个单位后得到的图象对应的解析式,其大于零的零点从小到大组成数列{xn},然后求解数列{xn}的前n项和Sn
个单位后得到的图象对应的解析式,其大于零的零点从小到大组成数列{xn},然后求解数列{xn}的前n项和Sn解答:解:(1)
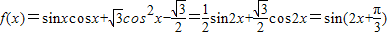 ,
,当
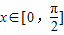 时,
时,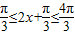 ,
,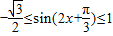 ,
,故值域为
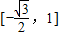 ,
,令
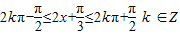 ,解得
,解得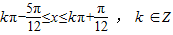 ,
,k=0时,解得
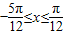 ,又
,又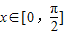
所以当
 上函数
上函数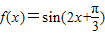 单调递增,
单调递增,令
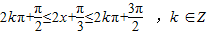 ,解得
,解得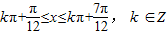 ,
,k=0时,解得
 ,,又
,,又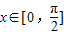
所以当
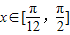 上函数
上函数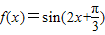 递减
递减综上,在区间
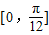 上函数
上函数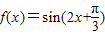 单调递增,在区间
单调递增,在区间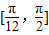 上函数
上函数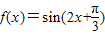 递减.
递减. (2)
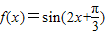 右平移
右平移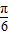 个单位后得到g(x)=sin2x,
个单位后得到g(x)=sin2x,令
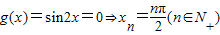 ,数列{xn}是以
,数列{xn}是以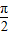 为首项,以
为首项,以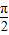 为公差的等差数列
为公差的等差数列故其前n项和为
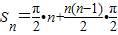 =
=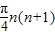 ,
,点评:本题考查三角函数的化简求值,二倍角公式与两角和的正弦函数的应用,考查函数与数列相结合的问题,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
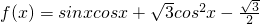
 上的单调区间和值域;
上的单调区间和值域; 个单位后得到的图象,其大于零的零点从小到大组成数列{xn},求数列{xn}的前n项和Sn.
个单位后得到的图象,其大于零的零点从小到大组成数列{xn},求数列{xn}的前n项和Sn.


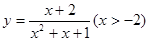
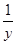 的取值范围;
的取值范围;