题目内容
已知向量 ,
, ,下面关于函数f(x)的导函数f'(x)说法中错误的是( )
,下面关于函数f(x)的导函数f'(x)说法中错误的是( )A.函数最小正周期是π
B.函数在区间
 为减函数
为减函数C.函数的图象关于直线
 对称
对称D.图象可由函数y=2sin2x向左平移
 个单位长度得到
个单位长度得到
【答案】分析:A:根据函数的解析式可得:f′(x)的最小正周期为:π.
B:因为对于函数 的单调减区间为[kπ-
的单调减区间为[kπ- ,kπ+
,kπ+ ],所以f′(x)在区间
],所以f′(x)在区间 为减函数.
为减函数.
C:函数f′(x)=2cos(2x+ )的对称轴为:x=
)的对称轴为:x= ,k∈Z.
,k∈Z.
D:函数y=2sin2x向左平移 个单位长度得到函数y=2sin(2x-
个单位长度得到函数y=2sin(2x- ),再根据诱导公式可得此答案正确.
),再根据诱导公式可得此答案正确.
解答:解:因为 ,
,
所以 =
= =sin(2x+
=sin(2x+ )+
)+ ,
,
所以f′(x)=2cos(2x+ ).
).
所以f′(x)的最小正周期为:π,所以A正确.
因为对于函数 的单调减区间为2kπ≤2x+
的单调减区间为2kπ≤2x+ ≤2kπ+π,即kπ-
≤2kπ+π,即kπ- ≤x≤kπ+
≤x≤kπ+ ,
,
所以f′(x)在区间 为减函数,所以B正确.
为减函数,所以B正确.
函数f′(x)=2cos(2x+ )的对称轴为:x=
)的对称轴为:x= ,k∈Z,所以C错误.
,k∈Z,所以C错误.
D:函数y=2sin2x向左平移 个单位长度得到函数y=2sin(2x-
个单位长度得到函数y=2sin(2x- ),再根据诱导公式可得此答案正确.
),再根据诱导公式可得此答案正确.
故选C.
点评:本题主要考查了余弦函数的有关性质,考查了学生对三角函数基础知识的理解和把握.
B:因为对于函数
 的单调减区间为[kπ-
的单调减区间为[kπ- ,kπ+
,kπ+ ],所以f′(x)在区间
],所以f′(x)在区间 为减函数.
为减函数.C:函数f′(x)=2cos(2x+
 )的对称轴为:x=
)的对称轴为:x= ,k∈Z.
,k∈Z.D:函数y=2sin2x向左平移
 个单位长度得到函数y=2sin(2x-
个单位长度得到函数y=2sin(2x- ),再根据诱导公式可得此答案正确.
),再根据诱导公式可得此答案正确.解答:解:因为
 ,
,所以
 =
= =sin(2x+
=sin(2x+ )+
)+ ,
,所以f′(x)=2cos(2x+
 ).
).所以f′(x)的最小正周期为:π,所以A正确.
因为对于函数
 的单调减区间为2kπ≤2x+
的单调减区间为2kπ≤2x+ ≤2kπ+π,即kπ-
≤2kπ+π,即kπ- ≤x≤kπ+
≤x≤kπ+ ,
,所以f′(x)在区间
 为减函数,所以B正确.
为减函数,所以B正确.函数f′(x)=2cos(2x+
 )的对称轴为:x=
)的对称轴为:x= ,k∈Z,所以C错误.
,k∈Z,所以C错误.D:函数y=2sin2x向左平移
 个单位长度得到函数y=2sin(2x-
个单位长度得到函数y=2sin(2x- ),再根据诱导公式可得此答案正确.
),再根据诱导公式可得此答案正确.故选C.
点评:本题主要考查了余弦函数的有关性质,考查了学生对三角函数基础知识的理解和把握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
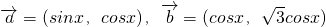 ,
,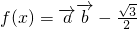 ,下面关于函数f(x)的导函数f'(x)说法中错误的是
,下面关于函数f(x)的导函数f'(x)说法中错误的是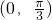 为减函数
为减函数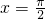 对称
对称 个单位长度得到
个单位长度得到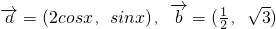 ,
, ,下面关于的说法中正确的是
,下面关于的说法中正确的是 为增函数
为增函数 对称
对称 个单位长度得到
个单位长度得到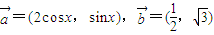 ,
,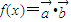 ,下面关于的说法中正确的是( )
,下面关于的说法中正确的是( )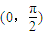 为增函数
为增函数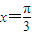 对称
对称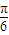 个单位长度得到
个单位长度得到