题目内容
已知A(-1,0,1),B(x,1,4),C(1,4,7),D(1,1,2),且A,B,C,D四点在同一平面上,则实数x等于分析:利用向量的坐标公式求出向量的坐标,利用四点共面的充要条件:由同一点出发,其它三点为终点的三个向量共线,列出方程求出x.
解答:解:
=(x+1,1,3)
=(2,4,6)
=(2,1,1),
∵A,B,C,D四点在同一平面上,
∴
,
,
共面,
∴存在m,n使,
=m
+n
即
解得x=-5,
故答案为:-5.
| AB |
| AC |
| AD |
∵A,B,C,D四点在同一平面上,
∴
| AB |
| AC |
| AD |
∴存在m,n使,
| AB |
| AC |
| AD |
即
|
故答案为:-5.
点评:本题考查向量的坐标公式、三向量共面的充要条件:其中一个向量可以用令两个向量线性表示.

练习册系列答案
相关题目
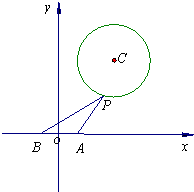 如图,在平面直角坐标系内,已知A(1,0),B(-1,0)两点,且圆C的方程为x2+y2-6x-8y+21=0,点P为圆上的动点.
如图,在平面直角坐标系内,已知A(1,0),B(-1,0)两点,且圆C的方程为x2+y2-6x-8y+21=0,点P为圆上的动点.