题目内容
一弹簧挂着小球作上下振动,经研究表明,时间x(s)与小球相对于平衡位置的高度y(cm)=f(x)的函数关系式符合某一正弦曲线f(x)=Asin(ωx+φ) (其中Α>0,ω>0,|φ|≤π),且离平衡位置最高点为(2,
),由最高点到相邻下一次图象交x轴于点(6,0); (1)求经多少时间小球往复振动一次?(2)确定g(x)表达式,使其图象与f(x)关于直线x=1对称.
| 2 |
由题意正弦曲线f(x)=Asin(ωx+φ) (其中Α>0,ω>0,|φ|≤π),
且离平衡位置最高点为(2,
),由最高点到相邻下一次图象交x轴于点(6,0);
可知A=
,T=16,所以ω=
,因为函数经过(6,0);
所以 0=
sin(
×6+φ),φ=
,f(x)=
sin(
x+
).
(1)有函数的周期可知,求经16,小球往复振动一次.
(2)f(x)关于直线x=1对称.所以(x,y)与(2-x,y)关于x=1对称,
所以所求的解析式g(x)=
sin(-
x+
)=
cos
x.
即g(x)=
cos
x.
且离平衡位置最高点为(2,
| 2 |
可知A=
| 2 |
| π |
| 8 |
所以 0=
| 2 |
| π |
| 8 |
| π |
| 4 |
| 2 |
| π |
| 8 |
| π |
| 4 |
(1)有函数的周期可知,求经16,小球往复振动一次.
(2)f(x)关于直线x=1对称.所以(x,y)与(2-x,y)关于x=1对称,
所以所求的解析式g(x)=
| 2 |
| π |
| 8 |
| π |
| 2 |
| 2 |
| π |
| 8 |
即g(x)=
| 2 |
| π |
| 8 |

练习册系列答案
相关题目
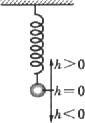
 ),由最高点到相邻下一次图象交x轴于点(6,0); (1)求经多少时间小球往复振动一次?(2)确定g(x)表达式,使其图象与f(x)关于直线x=1对称.
),由最高点到相邻下一次图象交x轴于点(6,0); (1)求经多少时间小球往复振动一次?(2)确定g(x)表达式,使其图象与f(x)关于直线x=1对称.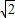 ),由最高点到相邻下一次图象交x轴于点(6,0); (1)求经多少时间小球往复振动一次?(2)确定g(x)表达式,使其图象与f(x)关于直线x=1对称.
),由最高点到相邻下一次图象交x轴于点(6,0); (1)求经多少时间小球往复振动一次?(2)确定g(x)表达式,使其图象与f(x)关于直线x=1对称.