题目内容
设y=8x2-lnx,则此函数在区间(0,
)和(
,1)内分别( )
| 1 |
| 4 |
| 1 |
| 2 |
| A、单调递增,单调递减 |
| B、单调递增,单调递增 |
| C、单调递减,单调递增 |
| D、单调递减,单调递减 |
分析:根据y=8x2-lnx,求导,根据不等式的基本性质分析导函数在区间(0,
)和(
,1)内的符号,确定函数的单调性.
| 1 |
| 4 |
| 1 |
| 2 |
解答:解:y′=16x-
.
当x∈(0,
)时,y′<0,y=8x2-lnx为减函数;
当x∈(
,1)时,y′>0,y=8x2-lnx为增函数.
故选C.
| 1 |
| x |
当x∈(0,
| 1 |
| 4 |
当x∈(
| 1 |
| 2 |
故选C.
点评:考查利用导数研究函数的单调性,注意导数的符号和原函数的单调区间之间的关系,以及函数的定义域,属基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
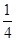 )内为( )
)内为( ) )和(
)和( ,1)内分别( )
,1)内分别( ) )和(
)和( ,1)内分别( )
,1)内分别( )