题目内容
13.求证:函数f(x)=$\sqrt{1+{x}^{2}}$-x在R上是单凋减函数.分析 根据已知中函数的解析式,求出函数的导函数,分析导函数的符号,可得函数的单调性.
解答 证明:∵f(x)=$\sqrt{1+{x}^{2}}$-x,
∴f′(x)=$\frac{x}{\sqrt{1+{x}^{2}}}$-1=$\frac{x-\sqrt{1+{x}^{2}}}{\sqrt{1+{x}^{2}}}$,
当x≤0时,易得f′(x)<0,
当x>0时,$\sqrt{1+{x}^{2}}$>x,此时f′(x)<0,
综上,f′(x)<0在R上恒成立,
故函数f(x)=$\sqrt{1+{x}^{2}}$-x在R上是单凋减函数.
点评 本题考查的知识点是函数单调性的判断与证明,单调性的证明一般有三种途径:定义法,性质,导数法,本题用导数法相对简单.

练习册系列答案
相关题目
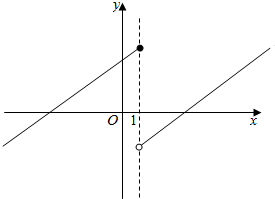 函数y=f(x)的图象如图所示,试写出函数y=f(x)的单调递增区间是(-∞,1],(1,+∞).
函数y=f(x)的图象如图所示,试写出函数y=f(x)的单调递增区间是(-∞,1],(1,+∞).