题目内容
已知椭圆 ,过椭圆右焦点F的直线L交椭圆于A、B两点,交y轴于P点.设
,过椭圆右焦点F的直线L交椭圆于A、B两点,交y轴于P点.设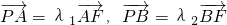 ,则λ1+λ2等于
,则λ1+λ2等于
- A.
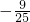
- B.
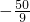
- C.
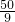
- D.

B
分析:设出直线方程,代入椭圆方程,利用韦达定理,结合向量条件,即可得到结论.
解答:由题意a=5,b=3,c=4,所以F点坐标为(4,0)
设直线l方程为:y=k(x-4),A点坐标为(x1,y1),B点坐标为(x2,y2),得P点坐标(0,-4k),
因为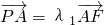 ,所以(x1,y1+4k)=λ1(4-x1,-y1)
,所以(x1,y1+4k)=λ1(4-x1,-y1)
因为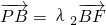 ,所以(x2,y2+4k)=λ2(4-x2,-y2).
,所以(x2,y2+4k)=λ2(4-x2,-y2).
得λ1= ,λ2=
,λ2= .
.
直线l方程,代入椭圆 ,消去y可得(9+25k2)x2-200k2x+400k2-225=0.
,消去y可得(9+25k2)x2-200k2x+400k2-225=0.
所以x1+x2= ,x1x2=
,x1x2=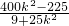 .
.
所以λ1+λ2= =
= =
= =
=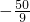
故选B.
点评:本题考查直线与椭圆的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.
分析:设出直线方程,代入椭圆方程,利用韦达定理,结合向量条件,即可得到结论.
解答:由题意a=5,b=3,c=4,所以F点坐标为(4,0)
设直线l方程为:y=k(x-4),A点坐标为(x1,y1),B点坐标为(x2,y2),得P点坐标(0,-4k),
因为
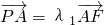 ,所以(x1,y1+4k)=λ1(4-x1,-y1)
,所以(x1,y1+4k)=λ1(4-x1,-y1)因为
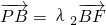 ,所以(x2,y2+4k)=λ2(4-x2,-y2).
,所以(x2,y2+4k)=λ2(4-x2,-y2).得λ1=
 ,λ2=
,λ2= .
.直线l方程,代入椭圆
 ,消去y可得(9+25k2)x2-200k2x+400k2-225=0.
,消去y可得(9+25k2)x2-200k2x+400k2-225=0.所以x1+x2=
 ,x1x2=
,x1x2=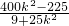 .
.所以λ1+λ2=
 =
= =
= =
=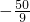
故选B.
点评:本题考查直线与椭圆的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C:
