Question

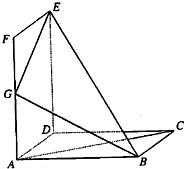如图所示，正方形ABCD和矩形ADEF所在平面相互垂直，G是AF的中点．
（I）求证：ED⊥AC；
（Ⅱ）若直线BE与平面ABCD成45°角，求异面直线GE与AC所成角的余弦值．

Answer 1

分析：（I）由矩形ADEF可知ED⊥AD，又因为平面ADEF⊥平面ABCD，得到ED⊥平面ABCD，从而有ED⊥AC．
（Ⅱ）由（I）ED⊥平面ABCD，可知∠EDB是直线BE与平面ABCD所成的角，又由AM∥GE，知∠MAC是异面直线GE与AC所成角或其补角
然后在△MAC中用余弦定理求解．

解答：（I）证明：在矩形ADEF中，ED⊥AD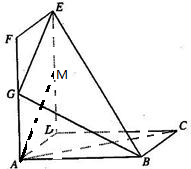
∵平面ADEF⊥平面ABCD，且平面ADEF∩平面ABCD=AD
∴ED⊥平面ABCD∴ED⊥AC（6分）

（Ⅱ）由（I）知：ED⊥平面ABCD
∴∠EBD是直线BE与平面ABCD所成的角，即∠EBD=45°（8分）
设AB=a，则DE=BD=

2

a
取DE中点M，连接AM
∵G是AF的中点∴AM∥GE
∴∠MAC是异面直线GE与AC所成角或其补角（10分）
连接BD交AC于点O
∵AM=CM=

a2+( 2 2 a)2

=

6

2

a，O是AC的中点
∴MO⊥AC
∴cos∠MAC=

AO

AM

=

2 2 a

6 2 a

=

3

3

，
∴异面直线GE与AC所成角的余弦值为

3

3

．（12分）

点评：本题主要考查线线垂直，线面垂直，面面垂直间的转化以及异面直线所成的角的求法．