题目内容
在如图所示五个图所表示的正方体中,能够得到AB⊥CD的是( )


分析:设图中正方体的棱长为1,建立空间坐标系,求出五个图中,向量
和
的坐标,代入向量数量积公式,判断其数量积是否为0,即可得到对应的线段是否垂直.
| AB |
| CD |
解答:解:设图中正方体的棱长为1,建立如图所示的空间坐标系: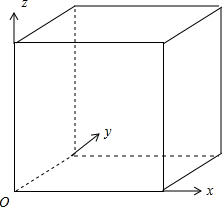
则①中,
=(0,1,-1),
=(0,-1,-1),
•
=0,故AB⊥CD成立;
②中,
=(1,-1,-1),
=(0,1,-1),
•
=0,故AB⊥CD成立;
③中,
=(0,-1,-1),
=(1,0,-1),
•
=1,故AB⊥CD不成立;
④中,
=(1,-1,-1),
=(0,1,0),
•
=-1,故AB⊥CD不成立;
⑤中,
=(1,0,0),
=(1,1,-1),
•
=1,故AB⊥CD不成立;
故能够得到AB⊥CD的是①②
故选A

则①中,
| AB |
| CD |
| AB |
| CD |
②中,
| AB |
| CD |
| AB |
| CD |
③中,
| AB |
| CD |
| AB |
| CD |
④中,
| AB |
| CD |
| AB |
| CD |
⑤中,
| AB |
| CD |
| AB |
| CD |
故能够得到AB⊥CD的是①②
故选A
点评:本题考查的知识点是空间中直线与直线之间的位置关系,其中建立空间坐标系,将线线有关系转化为空间向量垂直问题是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
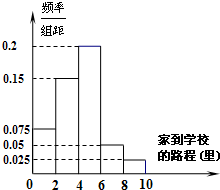 某高中地处县城,学校规定家到学校的路程在10里以内的学生可以走读,因交通便利,所以走读生人数很多.该校学生会先后5次对走读生的午休情况作了统计,得到如下资料:
某高中地处县城,学校规定家到学校的路程在10里以内的学生可以走读,因交通便利,所以走读生人数很多.该校学生会先后5次对走读生的午休情况作了统计,得到如下资料:①若把家到学校的距离分为五个区间:[0,2)、[2,4)、[4,6)、[6,8)、[8,10),则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如图所示的频率分布直方图;
②走读生是否午休与下午开始上课的时间有着密切的关系.下表是根据5次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
| 下午开始上课时间 | 1:30 | 1:40 | 1:50 | 2:00 | 2:10 |
| 平均每天午休人数 | 250 | 350 | 500 | 650 | 750 |
(Ⅱ)如果把下午开始上课时间1:30作为横坐标0,然后上课时间每推迟10分钟,横坐标x增加1,并以平均每天午休人数作为纵坐标y,试列出x与y的统计表,并根据表中的数据求平均每天午休人数
 |
| y |
 |
| y |
(Ⅲ)预测当下午上课时间推迟到2:20时,家距学校的路程在6里路以上的走读生中约有多少人午休?
(注:线性回归直线方程系数公式b=
| |||||||
|
| |||||||
|
. |
| y |
. |
| x |
某高中地处县城,学校规定家到学校的路程在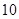 里
里
以内的学生可以走读,因交通便利,所以走读生人数很多,
该校学生会先后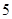 次对走读生的午休情况作了统计,得到
次对走读生的午休情况作了统计,得到
如下资料:
①若把家到学校的距离分为五个区间: 、
、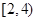 、
、 、
、 、
、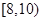 ,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图;
,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图;
②走读生是否午休与下午开始上课的时间有着密切的关系. 下表是根据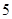 次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
|
下午开始上课时间 |
|
|
|
|
|
|
平均每天午休人数 |
|
|
|
|
|
(Ⅰ)若随机地调查一位午休的走读生,其家到学校的路程(单位:里)在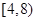 的概率是多少?
的概率是多少?
(Ⅱ)如果把下午开始上课时间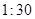 作为横坐标
作为横坐标 ,然后上课时间每推迟
,然后上课时间每推迟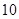 分钟,横坐标
分钟,横坐标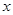 增加2,并以平均每天午休人数作为纵坐标
增加2,并以平均每天午休人数作为纵坐标 ,试列出
,试列出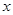 与
与 的统计表,并根据表中的数据求平均每天午休人数
的统计表,并根据表中的数据求平均每天午休人数 与上课时间
与上课时间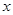 之间的线性回归方程
之间的线性回归方程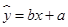 ;
;
(Ⅲ)预测当下午上课时间推迟到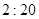 时,家距学校的路程在4里路以下的走读生中约有多少人午休?
时,家距学校的路程在4里路以下的走读生中约有多少人午休?
(注:线性回归直线方程系数公式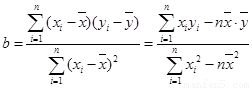 )
)
某高中地处县城,学校规定家到学校的路程在10里以内的学生可以走读,因交通便利,所以走读生人数很多.该校学生会先后5次对走读生的午休情况作了统计,得到如下资料:
①若把家到学校的距离分为五个区间:[0,2)、[2,4)、[4,6)、[6,8)、[8,10),则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如图所示的频率分布直方图;
②走读生是否午休与下午开始上课的时间有着密切的关系.下表是根据5次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
(Ⅰ)若随机地调查一位午休的走读生,其家到学校的路程(单位:里)在[2,6)的概率是多少?
(Ⅱ)如果把下午开始上课时间1:30作为横坐标0,然后上课时间每推迟10分钟,横坐标x增加1,并以平均每天午休人数作为纵坐标y,试列出x与y的统计表,并根据表中的数据求平均每天午休人数 与上课时间x之间的线性回归方程
与上课时间x之间的线性回归方程 =bx+a;
=bx+a;
(Ⅲ)预测当下午上课时间推迟到2:20时,家距学校的路程在6里路以上的走读生中约有多少人午休?

①若把家到学校的距离分为五个区间:[0,2)、[2,4)、[4,6)、[6,8)、[8,10),则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如图所示的频率分布直方图;
②走读生是否午休与下午开始上课的时间有着密切的关系.下表是根据5次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
| 下午开始上课时间 | 1:30 | 1:40 | 1:50 | 2:00 | 2:10 |
| 平均每天午休人数 | 250 | 350 | 500 | 650 | 750 |
(Ⅱ)如果把下午开始上课时间1:30作为横坐标0,然后上课时间每推迟10分钟,横坐标x增加1,并以平均每天午休人数作为纵坐标y,试列出x与y的统计表,并根据表中的数据求平均每天午休人数
 与上课时间x之间的线性回归方程
与上课时间x之间的线性回归方程 =bx+a;
=bx+a;(Ⅲ)预测当下午上课时间推迟到2:20时,家距学校的路程在6里路以上的走读生中约有多少人午休?

某高中地处县城,学校规定家到学校的路程在10里以内的学生可以走读,因交通便利,所以走读生人数很多.该校学生会先后5次对走读生的午休情况作了统计,得到如下资料:
①若把家到学校的距离分为五个区间:[0,2)、[2,4)、[4,6)、[6,8)、[8,10),则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如图所示的频率分布直方图;
②走读生是否午休与下午开始上课的时间有着密切的关系.下表是根据5次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
(Ⅰ)若随机地调查一位午休的走读生,其家到学校的路程(单位:里)在[2,6)的概率是多少?
(Ⅱ)如果把下午开始上课时间1:30作为横坐标0,然后上课时间每推迟10分钟,横坐标x增加1,并以平均每天午休人数作为纵坐标y,试列出x与y的统计表,并根据表中的数据求平均每天午休人数 与上课时间x之间的线性回归方程
与上课时间x之间的线性回归方程 =bx+a;
=bx+a;
(Ⅲ)预测当下午上课时间推迟到2:20时,家距学校的路程在6里路以上的走读生中约有多少人午休?

①若把家到学校的距离分为五个区间:[0,2)、[2,4)、[4,6)、[6,8)、[8,10),则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如图所示的频率分布直方图;
②走读生是否午休与下午开始上课的时间有着密切的关系.下表是根据5次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
| 下午开始上课时间 | 1:30 | 1:40 | 1:50 | 2:00 | 2:10 |
| 平均每天午休人数 | 250 | 350 | 500 | 650 | 750 |
(Ⅱ)如果把下午开始上课时间1:30作为横坐标0,然后上课时间每推迟10分钟,横坐标x增加1,并以平均每天午休人数作为纵坐标y,试列出x与y的统计表,并根据表中的数据求平均每天午休人数
 与上课时间x之间的线性回归方程
与上课时间x之间的线性回归方程 =bx+a;
=bx+a;(Ⅲ)预测当下午上课时间推迟到2:20时,家距学校的路程在6里路以上的走读生中约有多少人午休?


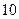 里
里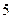 次对走读生的午休情况作了统计,得到
次对走读生的午休情况作了统计,得到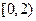 、
、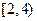 、
、 、
、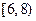 、
、 ,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图;
,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图;



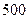
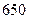

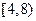 的概率是多少?
的概率是多少? ,然后上课时间每推迟
,然后上课时间每推迟 增加2,并以平均每天午休人数作为纵坐标
增加2,并以平均每天午休人数作为纵坐标 ,试列出
,试列出 与上课时间
与上课时间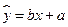 ;
; 时,家距学校的路程在4里路以下的走读生中约有多少人午休?
时,家距学校的路程在4里路以下的走读生中约有多少人午休?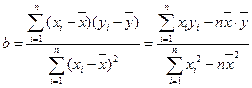 )
)