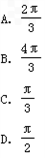题目内容
球O为长方体ABCD-A1B1C1D1的外接球,已知AB=2,AD=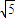 ,AA1=
,AA1=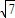 ,则顶点A、B间的球面距离是( )
,则顶点A、B间的球面距离是( )A.
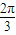
B.
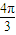
C.
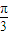
D.
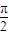
【答案】分析:先求长方体的对角线,就是球的直径,再求所对AB的球心角,然后求A、B间的球面距离.
解答:解:∵AB=2,AD=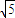 ,AA1=
,AA1=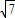 ,
,
∴长方体的对角线,即球的直径2R=4,
设BD1∩AC1=O,则OA=OB=R=AB,∴∠AOB=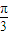 ,
,
∴l=Rθ=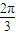 ,
,
故选A.
点评:本题考查球的内接体问题,考查学生空间想象能力,逻辑思维能力,是基础题.
解答:解:∵AB=2,AD=
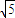 ,AA1=
,AA1=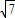 ,
,∴长方体的对角线,即球的直径2R=4,
设BD1∩AC1=O,则OA=OB=R=AB,∴∠AOB=
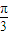 ,
,∴l=Rθ=
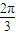 ,
,故选A.
点评:本题考查球的内接体问题,考查学生空间想象能力,逻辑思维能力,是基础题.

练习册系列答案
相关题目
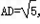
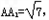 则顶点A 、B 间的球面距离是
则顶点A 、B 间的球面距离是