题目内容
下面有4个命题:①当(1+4k2)x2+8kmx+4m2-4=0时,2x+
| 1 |
| 2x |
②若双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
③将函数y=cos2x的图象向右平移
| π |
| 6 |
| π |
| 6 |
其中 错误命题的序号为
分析:①如果方程无实数解时,结论不一定成立故可判断出①错误;②中根据渐近线方程求得a和b的关系,利用抛物线求得焦点坐标,求得a和b的另一关系式,最后联立求得a和b,则c可求得,进而求得双曲线的离心率,判断出②正确;③利用三角函数图象平移的法则可推断出③不正确.
解答:解:①若方程的判别式小于0,方程无实数解时,2x+
的最小值就不是2了.故①错误;
②依题意可知
求得a=1,b=
∴c=
=2,e=
=2,故②正确.
③将函数y=cos2x的图象向右平移
个单位,可得到y=cos(2x-
)的图象,故③错误.
故答案为:①③
| 1 |
| 2x |
②依题意可知
|
| 3 |
∴c=
| 3+1 |
| c |
| a |
③将函数y=cos2x的图象向右平移
| π |
| 6 |
| π |
| 3 |
故答案为:①③
点评:本题主要考查了双曲线的简单性质,二次函数的性质和三角函数的图象变换.考查了学生对基础知识的综合掌握.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
 的最小值为2;
的最小值为2; 的一条渐近线方程为
的一条渐近线方程为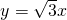 ,且其一个焦点与抛物线y2=8x的焦点重合,则双曲线的离心率为2;
,且其一个焦点与抛物线y2=8x的焦点重合,则双曲线的离心率为2; 个单位,可以得到函数
个单位,可以得到函数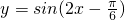 的图象;
的图象;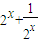 的最小值为2;
的最小值为2;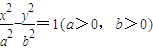 的一条渐近线方程为
的一条渐近线方程为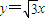 ,且其一个焦点与抛物线y2=8x的焦点重合,则双曲线的离心率为2;
,且其一个焦点与抛物线y2=8x的焦点重合,则双曲线的离心率为2;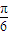 个单位,可以得到函数
个单位,可以得到函数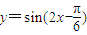 的图象;
的图象;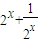 的最小值为2;
的最小值为2;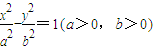 的一条渐近线方程为
的一条渐近线方程为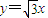 ,且其一个焦点与抛物线y2=8x的焦点重合,则双曲线的离心率为2;
,且其一个焦点与抛物线y2=8x的焦点重合,则双曲线的离心率为2; 个单位,可以得到函数
个单位,可以得到函数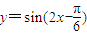 的图象;
的图象;