题目内容
已知抛物线y2=4x与直线x+y-2=0的交点为A,B,抛物线的顶点为O,在抛物线弧AOB上求一点C,使△ABC的面积最大,并求出这个最大面积.
答案:
解析:
解析:
|
解析:如下图,设与直线AB平行且与抛物线相切的直线方程为x+y-b=0.
将它与抛物线方程y2=4x联立,得y2=4(b-y). 即y2+4y-4b=0 由Δ=42-4(-4b)=0,b=-1,若切线为x+y+1=0,求得切点为C(1,-2),因直线x+y+1=0与x+y-2=0的距离为d= 解得交点坐标为A( B( ∴|AB|= S△ABC= 即当C点为(1,-2)时,S△ABC的最大值为 分析:利用直线与曲线关系、最值问题、点到直线的距离公式求解. |

练习册系列答案
相关题目

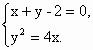
 -
- =1(a>0,b>0)的左顶点,且此双曲线的一条渐
=1(a>0,b>0)的左顶点,且此双曲线的一条渐 B.2
B.2 D.2
D.2