题目内容
7.在锐角△ABC中,A,B,C为三角形的三个内角,已知A>B>C,则cosB取值范围为(0,$\frac{\sqrt{2}}{2}$).分析 锐角△ABC中,由A>B>C,B+C>90°,先求得B的范围,从而求得cosB取值范围.
解答 解:在锐角△ABC中,∵A>B>C,∴B+C>90°,∴45°<B<90°,
则cosB取值范围为(0,$\frac{\sqrt{2}}{2}$),
故答案为:(0,$\frac{\sqrt{2}}{2}$).
点评 本题主要考查锐角三角形的性质,余弦函数的定义域和值域,属于基础题.

练习册系列答案
相关题目
17.如图所示的三个直角三角形是一个体积为20cm3的几何体的三视图,则h=( )cm.
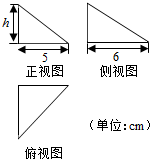

| A. | 4 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
18.平行四边形ABCD中,点P在边AB上(不含端点),$\overrightarrow{AP}=λ\overrightarrow{AB}$.若|$\overrightarrow{AP}$|=2,|$\overrightarrow{AD}$|=1,∠BAD=60°且$\overrightarrow{AP}•\overrightarrow{CP}$=-3.则λ=( )
| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
2.已知F为抛物线y2=2px(p>0)的焦点,过F的直线l交抛物线于A(x1,y1)、B(x2,y2),O为坐标原点,若△OAB的面积为p2,则y12+y22的值为( )
| A. | 10p2 | B. | 12p2 | C. | 14p2 | D. | 16p2 |
2.已知等比数列{an}中,a3a5+2a4a6+a5a7=49,则a4+a6=( )
| A. | 14 | B. | ±7 | C. | 7 | D. | -14 |
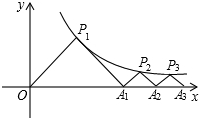 如图所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函数y=$\frac{4}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3…△PnAn-1An…都是等腰直角三角形,斜边OA1,A1A2…An-1An,都在x轴上,则y1+y2+…y10=$2\sqrt{10}$.
如图所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函数y=$\frac{4}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3…△PnAn-1An…都是等腰直角三角形,斜边OA1,A1A2…An-1An,都在x轴上,则y1+y2+…y10=$2\sqrt{10}$. 已知函数$f(x)=\frac{1}{3}a{x^3}+({a-2})x+c$的图象如图所示.
已知函数$f(x)=\frac{1}{3}a{x^3}+({a-2})x+c$的图象如图所示.