Question

关于x的方程x+2^x=2，x+log₂x=2的解分别为α、β，根据指数函数和对数函数的图象，α+β=

 

．

Answer 1

分析：将方程x+2^x=2的根，转化为两个函数y=-x与y=2^x-2的交点，同样将方程x+log₂x=2的根，转化为两个函数y=-x与y=log₂x-2的交点，可以发现是y=2^x-2与y=log₂x-2同时与y=-x的交点的横坐标之和如图可解．

解答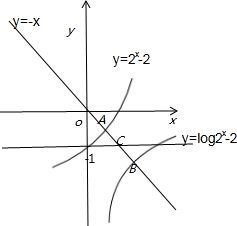：解：将x+2^x=2，变形为：-x=2^x-2，
令：y=-x与y=2^x-2，
将x+log₂x=2，变形为：-x=log₂x-2，
令y=-x与y=log₂x-2，
如图所示：C为线段AB的中点，即：xC=

xA+xB

2

，
∴α+β=2．

点评：本题主要考查方程的根即为相应函数图象交点的横坐标，还考查了函数思想，转化思想，数形结合思想．