题目内容
已知抛物线y2=4ax(0<a<1=的焦点为F,以A(a+4,0)为圆心,|AF|为半径在x轴上方作半圆交抛物线于不同的两点M和N,设P为线段MN的中点.
(1)求|MF|+|NF|的值;
(2)是否存在这样的a值,使|MF|、|PF|、|NF|成等差数列?如存在,求出a的值,若不存在,说明理由.
(1)求|MF|+|NF|的值;
(2)是否存在这样的a值,使|MF|、|PF|、|NF|成等差数列?如存在,求出a的值,若不存在,说明理由.
分析:(1)先设M(x1,y1),N(x2,y2),P(x0,y0),根据抛物线的方程可得到F(a,0),然后联立抛物线与圆的方程消去y得到关于x的一元二次方程,进而可得到两根之和,即可得到|MF|+|NF|的值.
(2)先假设存在a满足条件,根据2|PF|=|MF|+|NF|,再由抛物线的定义可得到|PF|=4x0=4-a,将x0代入圆的方程,求出的y0值,故可得到a的值,但与点P是弦MN的中点得到的a的范围矛盾,可得到结论.
(2)先假设存在a满足条件,根据2|PF|=|MF|+|NF|,再由抛物线的定义可得到|PF|=4x0=4-a,将x0代入圆的方程,求出的y0值,故可得到a的值,但与点P是弦MN的中点得到的a的范围矛盾,可得到结论.
解答:解:(1)F(a,0),设M(x1,y1),N(x2,y2),P(x0,y0),
由 {,
,消去y,得
⇒x2+2(a-4)x+(a2+8a)=0,
∵△>0,∴x1+x2=2(4-a),
∴|MF|+|NF|=(x1+a)+(x2+a)=8.
(2)假设存在a值,使的|MF|,|PF|,|NF|成等差数列,即2|PF|=|MF|+|NF|⇒|PF|=4x0=4-a,
∴
又
=
=a(x1+x2)+2a
=2a(4-a)+2a
⇒
2a(4-a)+2a
=16a-4a2⇒a=2,
与
⇒0<a<1矛盾.
∴假设不成立.
即不存在a值,使的|MF|,|PF|,|NF|成等差数列.
由 {,
|
⇒x2+2(a-4)x+(a2+8a)=0,
∵△>0,∴x1+x2=2(4-a),
∴|MF|+|NF|=(x1+a)+(x2+a)=8.
(2)假设存在a值,使的|MF|,|PF|,|NF|成等差数列,即2|PF|=|MF|+|NF|⇒|PF|=4x0=4-a,
∴
|
又
|
=
4ax1+4ax2+2
| ||||
| 4 |
| x1x2 |
=2a(4-a)+2a
| a2+8a |
2a(4-a)+2a
| a2+8a |
与
|
∴假设不成立.
即不存在a值,使的|MF|,|PF|,|NF|成等差数列.
点评:本题主要考查抛物线的基本性质、等差关系的确定等,考查综合运用能力和计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

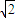 ,过抛物线C1的焦点F作倾斜角为
,过抛物线C1的焦点F作倾斜角为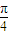 的直线l,交椭圆C于一点P(点P在x轴上方),交抛物线C1于一点Q(点Q在x轴下方).
的直线l,交椭圆C于一点P(点P在x轴上方),交抛物线C1于一点Q(点Q在x轴下方).