题目内容
求曲线y=x3+x-2与直线y=4x+3平行的切线方程.
分析:设出切点坐标(x0,y0),令f′(x0)=4,求出x0、y0,然后由点斜式求切线方程.
解:设切点为P0(x0,y0),则y0=x03+x0-2.①
又y′=3x2+1,切线斜率k=4,所以3x02+1=4.②
由①②,得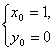
或
∴切线方程为y=4x或y=4x-4.
练习册系列答案
相关题目
题目内容
求曲线y=x3+x-2与直线y=4x+3平行的切线方程.
分析:设出切点坐标(x0,y0),令f′(x0)=4,求出x0、y0,然后由点斜式求切线方程.
解:设切点为P0(x0,y0),则y0=x03+x0-2.①
又y′=3x2+1,切线斜率k=4,所以3x02+1=4.②
由①②,得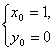或∴切线方程为y=4x或y=4x-4.