题目内容
已知平面区域Ω={(x,y)|x2+y2≤1},M={(x,y)||x|+|y|≤1},若在区域Ω上随机扔一个点P,则点P落在区域M的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:本题考查的知识点是几何概型的意义,关键是要找出(x,y)对应图形的面积,及满足条件“区域M”的点对应的图形的面积,然后再结合几何概型的计算公式进行求解.
解答: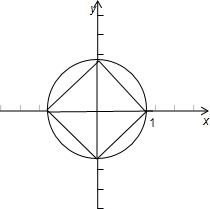 解:如图所示,区域Ω为图中正方形,
解:如图所示,区域Ω为图中正方形,
∵R=1,∴圆的面积为π
且圆内接正方形的对角线长为2R=2,
∴圆内接正方形的边长为
∴圆内接正方形的面积为2
则小豆落在正方形内的概率P=
故答案为A.
 解:如图所示,区域Ω为图中正方形,
解:如图所示,区域Ω为图中正方形,∵R=1,∴圆的面积为π
且圆内接正方形的对角线长为2R=2,
∴圆内接正方形的边长为
| 2 |
∴圆内接正方形的面积为2
则小豆落在正方形内的概率P=
| 2 |
| π |
故答案为A.
点评:本题考查的知识点是几何概型的意义,简单地说,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.

练习册系列答案
相关题目
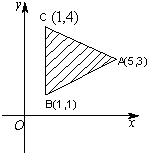 已知平面区域如图所示,z=x+my(m>0)在平面区域内取得最大值时的解(x,y)有无数多个,则m=
已知平面区域如图所示,z=x+my(m>0)在平面区域内取得最大值时的解(x,y)有无数多个,则m=