题目内容
(A题)已知x,y,z∈R+,且x+y+z=1.(1)求证:
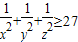 ;
;(2)若λ(x2+y2+z2)≤x3+y3+z3恒成立,求实数λ的最大值.
【答案】分析:(1)依题意,利用基本不等式1=x+y+z≥3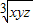 >0可求得0<
>0可求得0<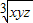 ≤
≤ ,同理即可证得
,同理即可证得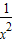 +
+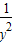 +
+ ≥27;
≥27;
(2)利用x3+y3+z3=(x3+y3+z3)(x+y+z)≥(x2+y2+z2)2及(x2+y2+z2)(12+12+12)≥(x+y+z)2=1,即可证得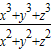 ≥
≥ ,而λ≤
,而λ≤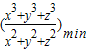 ,从而可得答案.
,从而可得答案.
解答:证明(1)∵x,y,z∈R+,且x+y+z=1,
∴1=x+y+z≥3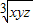 >0,
>0,
∴0<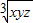 ≤
≤ ,
,
∴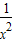 +
+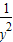 +
+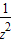 ≥
≥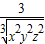 =
=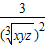 ≥
≥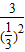 =27,
=27,
故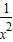 +
+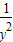 +
+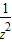 ≥27当且仅当x=y=z=
≥27当且仅当x=y=z= 时等号成立…(6分)
时等号成立…(6分)
(2)∵x,y,z∈R+,x+y+z=1且λ(x2+y2+z2)≤x3+y3+z3恒成立,
∴λ≤ 恒成立,
恒成立,
∵x3+y3+z3=(x3+y3+z3)(x+y+z)≥(x2+y2+z2)2,
又∵(x2+y2+z2)(12+12+12)≥(x+y+z)2=1,
∴x2+y2+z2≥ ,
,
∴x3+y3+z3≥ (x2+y2+z2)⇒
(x2+y2+z2)⇒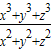 ≥
≥ ,当且仅当x=y=z=
,当且仅当x=y=z= 时等号成立.
时等号成立.
∴λ≤ ,故实数λ的最大值为
,故实数λ的最大值为 …(14分)
…(14分)
点评:本题考查不等式的证明,考查等价转化思想与函数思想,考查逻运算与辑推理证明的能力,属于难题.
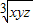 >0可求得0<
>0可求得0<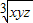 ≤
≤ ,同理即可证得
,同理即可证得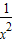 +
+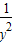 +
+ ≥27;
≥27;(2)利用x3+y3+z3=(x3+y3+z3)(x+y+z)≥(x2+y2+z2)2及(x2+y2+z2)(12+12+12)≥(x+y+z)2=1,即可证得
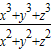 ≥
≥ ,而λ≤
,而λ≤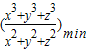 ,从而可得答案.
,从而可得答案.解答:证明(1)∵x,y,z∈R+,且x+y+z=1,
∴1=x+y+z≥3
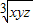 >0,
>0,∴0<
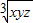 ≤
≤ ,
,∴
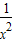 +
+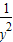 +
+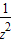 ≥
≥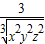 =
=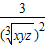 ≥
≥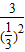 =27,
=27,故
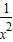 +
+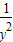 +
+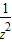 ≥27当且仅当x=y=z=
≥27当且仅当x=y=z= 时等号成立…(6分)
时等号成立…(6分)(2)∵x,y,z∈R+,x+y+z=1且λ(x2+y2+z2)≤x3+y3+z3恒成立,
∴λ≤
 恒成立,
恒成立,∵x3+y3+z3=(x3+y3+z3)(x+y+z)≥(x2+y2+z2)2,
又∵(x2+y2+z2)(12+12+12)≥(x+y+z)2=1,
∴x2+y2+z2≥
 ,
,∴x3+y3+z3≥
 (x2+y2+z2)⇒
(x2+y2+z2)⇒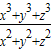 ≥
≥ ,当且仅当x=y=z=
,当且仅当x=y=z= 时等号成立.
时等号成立.∴λ≤
 ,故实数λ的最大值为
,故实数λ的最大值为 …(14分)
…(14分)点评:本题考查不等式的证明,考查等价转化思想与函数思想,考查逻运算与辑推理证明的能力,属于难题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 [选做题]在下面A,B,C,D四个小题中只能选做两题,每小题10分,共20分.
[选做题]在下面A,B,C,D四个小题中只能选做两题,每小题10分,共20分.