题目内容
8．已知cos（α-β）cosα+sin（α-β）sinα=-$\frac{4}{5}$，且β是第三象限的角，则sinβ=$-\frac{3}{5}$．分析 由两角差的余弦公式可得cosβ，进而由同角三角函数的基本关系可得．
解答 解：∵cos（α-β）cosα+sin（α-β）sinα=-$\frac{4}{5}$，
∴cos[（α-β）-α]=-$\frac{4}{5}$，即cosβ=-$\frac{4}{5}$，
∵β是第三象限的角，
∴sinβ=-$\sqrt{1-co{s}^{2}β}$=-$\frac{3}{5}$，
故答案为：$-\frac{3}{5}$．
点评 本题考查两角和与差的三角函数公式，涉及同角三角函数的基本关系，属基础题．
练习册系列答案
相关题目
已知函数$f（x）=2sin（2x+\frac{π}{6}）+1+a$，x∈[0，π]的最大值为2
3．已知集合A={-1，0，1，2}，集合B={x∈R|x2=1}，则A∩B=（ ）
| A． | {1} | B． | {-1，1} | C． | {-1，0，1} | D． | {-1，0，1，2} |
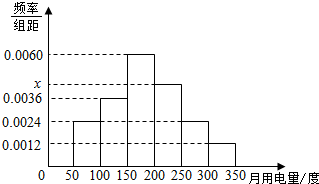为调查我校学生的用电情况，学校后勤部门组织抽取了100间学生宿舍某月用电量调查，发现每间宿舍用电量都在50度到350度之间，其频率分布直方图如图所示．