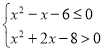题目内容
【题目】已知函数f(x)![]() ,x∈R.
,x∈R.
(1)若f(x)是偶函数,求实数a的值;
(2)当a>0时,不等式f(sinx![]() cosx)﹣f(4+t)≥0对任意的x∈
cosx)﹣f(4+t)≥0对任意的x∈![]() 恒成立,求实数t的取值范围;
恒成立,求实数t的取值范围;
(3)当a>0时,关于x的方程![]() 在区间[1,2]上恰有两个不同的实数解,求实数a的取值范围.
在区间[1,2]上恰有两个不同的实数解,求实数a的取值范围.
【答案】(1)a![]() ;(2)(
;(2)(![]() ];(3)(
];(3)(![]() ,log4
,log4![]() ]
]
【解析】
(1)根据f(x)是偶函数,有f(﹣x)=f(x),得log2(2﹣x+1)+a(﹣x)=log2(2x+1)+ax化简求解.
(2)由a>0,结合对数函数和一次函数的单调性,得到函数f(x)=log2(2x+1)+ax是增函数,然后利用单调性的定义,将不等式f(sinx![]() cosx)﹣f(4+t)≥0,转化为sinx
cosx)﹣f(4+t)≥0,转化为sinx![]() cosx≥4+t,对任意的x∈
cosx≥4+t,对任意的x∈![]() 恒成立,利用三角函数的性质求解.
恒成立,利用三角函数的性质求解.
(3)根据题意,有 f(0)=1,将方程f[f(x)﹣a(1+x)﹣1og4(2x﹣1)]=1,转化为f[f(x)﹣a(1+x)﹣1og4(2x﹣1)]=f(0).再利用函数的单调性,转化为变形为:1og4![]() a,通过函数g(x)的图象与y=a有2个交点求解.
a,通过函数g(x)的图象与y=a有2个交点求解.
(1)根据题意,若f(x)是偶函数,则f(﹣x)=f(x),
则有log2(2﹣x+1)+a(﹣x)=log2(2x+1)+ax,变形可得2ax=log2(2﹣x+1)﹣log2(2x+1)=﹣x,
解得a![]() ;
;
(2)当a>0时,函数y=log2(2x+1)和函数y=ax都是增函数,则函数f(x)=log2(2x+1)+ax为增函数,
∵不等式f(sinx![]() cosx)﹣f(4+t)≥0,所以f(
cosx)﹣f(4+t)≥0,所以f(![]() )≥f(4+t)对任意的x∈
)≥f(4+t)对任意的x∈![]() 恒成立
恒成立
∴sinx![]() cosx≥4+t,对任意的x∈
cosx≥4+t,对任意的x∈![]() 恒成立;
恒成立;
∴t≤2sin(x![]() )﹣4对任意的x∈
)﹣4对任意的x∈![]() 恒成立;
恒成立;
∴t≤(2sin(x![]() )﹣4)min,x∈
)﹣4)min,x∈![]() ;
;
由x∈![]() ,得x
,得x![]() ∈[
∈[![]() ],
],
∴当x![]() 时,sin(x
时,sin(x![]() )﹣4的最小值为
)﹣4的最小值为![]() 4;
4;
∴t![]() ;故t的取值范围为(
;故t的取值范围为(![]() ].
].
(3)根据题意,函数f(x)=log2(2x+1)+ax,有f(0)=1,
则f[f(x)﹣a(1+x)﹣1og4(2x﹣1)]=1即f[f(x)﹣a(1+x)﹣1og4(2x﹣1)]=f(0).
又由当a>0时,函数f(x)=log2(2x+1)+ax为增函数,
则有f(x)﹣a(1+x)﹣1og4(2x﹣1)=0,
即log2(2x+1)﹣1og4(2x﹣1)=a,
变形可得:1og4![]() a,设g(x)=1og4
a,设g(x)=1og4![]() ,
,
若方程f[f(x)﹣a(1+x)﹣1og4(2x﹣1)]=1在区间[1,2]上恰有两个不同的实数解,则函数g(x)的图象与y=a有2个交点,
对于g(x)=1og4![]() ,设h(x)
,设h(x)![]() ,则h(x)
,则h(x)![]() (2x﹣1)
(2x﹣1)![]() 4.
4.
又由1≤x≤2,则1≤2x﹣1≤3,则h(x)min=8,h(1)=9,h(2)![]() ,则h(x)max=9,
,则h(x)max=9,
若函数g(x)的图象与y=a有2个交点,
必有log48![]() a≤log4
a≤log4![]() ,
,
故a的取值范围为(![]() ,log4
,log4![]() ].
].