题目内容
小王经营一家面包店,每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元,若当天卖不完,则未卖出的现烤面包因过期每个亏损5元.经统计,得到在某月(30天)中,小王每天售出的现烤面包个数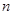 及天数如下表:
及天数如下表:
|
售出个数 |
10 |
11 |
12 |
13 |
14 |
15 |
|
天数 |
3 |
3 |
3 |
6 |
9 |
6 |
试依据以频率估计概率的统计思想,解答下列问题:
(Ⅰ)计算小王某天售出该现烤面包超过13个的概率;
(Ⅱ)若在今后的连续5天中,售出该现烤面包超过13个的天数大于3天,则小王决定增加订购量. 试求小王增加订购量的概率.
(Ⅲ)若小王每天订购14个该现烤面包,求其一天出售该现烤面包所获利润的分布列和数学期望.
(Ⅰ)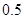 ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
【解析】
试题分析:(Ⅰ)利用古典概型的概率公式即可计算出题中事件的概率;(Ⅱ)根据题中的数据类型,确定随机变量满足二项分布,然后直接利用二项分布的概率计算方法可以计算题中事件的概率;(Ⅲ)将小王每天所获的利润的可能值列举出来,然后再根据相应值计算相应事件的概率,并列举出随机变量的概率分布列和计算随机变量的数学期望即可.
试题解析:(Ⅰ)记事件A=“小王某天售出超过13个现烤面包”, 1分
用频率估计概率可知:
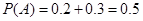 .
2分
.
2分
所以小王某天售出超过13个现烤面包的概率为0.5. 3分
(Ⅱ)设在最近的5天中售出超过13个的天数为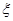 ,
,
则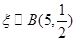 . 5分
. 5分
记事件B=“小王增加订购量”,
则有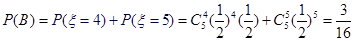 ,
,
所以小王增加订购量的概率为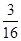 . 8分
. 8分
(Ⅲ)若小王每天订购14个现烤面包,设其一天的利润为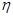 元,
元,
则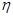 的所有可能取值为80,95,110,125,140. ..9分
的所有可能取值为80,95,110,125,140. ..9分
其分布列为
|
利润 |
80 |
95 |
110 |
125 |
140 |
|
概率 |
0.1 |
0.1 |
0.1 |
0.2 |
0.5 |
11分
则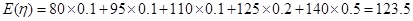
所以小王每天出售该现烤面包所获利润的数学期望为123.5元. ..13分
考点:古典概型、二项分布、随机变量的概率分布列与数学期望

| 售出个数n | 10 | 11 | 12 | 13 | 14 | 15 |
| 天数 | 3 | 3 | 3 | 6 | 9 | 6 |
(Ⅰ)计算小王某天售出该现烤面包超过13个的概率;
(Ⅱ)若在今后的连续5天中,售出该现烤面包超过13个的天数大于3天,则小王决定增加订购量.试求小王增加订购量的概率.
(Ⅲ)若小王每天订购14个该现烤面包,求其一天出售该现烤面包所获利润的分布列和数学期望.