题目内容
设函数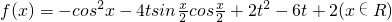
(1)当t=1时,求f(x)的最小值;
(2)若t∈R,将f(x)的最小值记为g(t),求g(t)的表达式;
(3)当-1≤t≤1时,关于t的方程g(t)=kt有且只有一个实根,求实数k的取值范围.
解:(1)当t=1时,f(x)=-cos2x-2sinx+2-6+2=sin2x-2sinx-3=(sinx-1)2-4,
故当sinx=1时,f(x)有最小值等于-4.
(2)若t∈R,∵f(x)=-cos2x-2tsinx+2t2-6t+2=sin2x-2tsinx+2t2-6t+1=(sinx-t)2+t2-6t+1,
且-1≤sinx≤1.
当t<-1时,则当sinx=-1时,f(x)取得最小值g(t)=(-1-t)2+t2-6t+1=2t2-4t+2.
当-1≤t≤1时,则当sinx=t时,f(x)的最小值g(t)=t2-6t+1.
当t>1时,则当sinx=1时,f(x)的最小值g(t)=(1-t)2+t2-6t+1=2t2-8t+2.
综上,g(t)=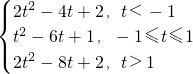 .
.
(3)当-1≤t≤1时,关于t的方程g(t)=kt 即 t2-6t+1=kt.由题意可得
关于t的方程 t2-6t+1-kt=0 在[-1,1]内有且只有一个实根,
①当△=(6+k)2-4=0时,应有-1≤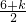 ≤1,解得 k=-4,或k=-8.
≤1,解得 k=-4,或k=-8.
若 k=-4,方程有两个相等的根t=1,若 k=-8,方程有两个相等的根t=-1.
②当△=(6+k)2-4>0时,即 k<-8,或k>-4时,
令h(t)=t2-6t+1-kt,由题意可得 h(-1)h(1)=(k+8)(-k-4)<0,解得 k<-8,或 k>-4.
综合①②可得,当k≥-4,或k≤-8 时,关于t的方程g(t)=kt有且只有一个实根.
故所求的实数k的取值范围为(-∞,-8[∪[-4,+∞).
分析:(1)当t=1时,f(x)=(sinx-1)2-4,故当sinx=1时,f(x)有最小值等于-4.
(2)若t∈R,由f(x)=(sinx-t)2+t2-6t+1,分t<-1、-1≤t≤1、t>1三种情况分别求出f(x)的
最小值g(t)的解析式.
(3)由题意可得方程 t2-6t+1-kt=0 在[-1,1]内有且只有一个实根,分△=0和△>0两种情况,分别求得求得
实数k的取值范围,再把得到的实数k的取值范围取并集,即得所求.
点评:本题考查三角函数的恒等变换及化简求值,三角函数的最值,体现了分类讨论的数学思想,属于中档题.
故当sinx=1时,f(x)有最小值等于-4.
(2)若t∈R,∵f(x)=-cos2x-2tsinx+2t2-6t+2=sin2x-2tsinx+2t2-6t+1=(sinx-t)2+t2-6t+1,
且-1≤sinx≤1.
当t<-1时,则当sinx=-1时,f(x)取得最小值g(t)=(-1-t)2+t2-6t+1=2t2-4t+2.
当-1≤t≤1时,则当sinx=t时,f(x)的最小值g(t)=t2-6t+1.
当t>1时,则当sinx=1时,f(x)的最小值g(t)=(1-t)2+t2-6t+1=2t2-8t+2.
综上,g(t)=
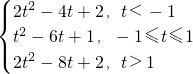 .
.(3)当-1≤t≤1时,关于t的方程g(t)=kt 即 t2-6t+1=kt.由题意可得
关于t的方程 t2-6t+1-kt=0 在[-1,1]内有且只有一个实根,
①当△=(6+k)2-4=0时,应有-1≤
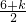 ≤1,解得 k=-4,或k=-8.
≤1,解得 k=-4,或k=-8.若 k=-4,方程有两个相等的根t=1,若 k=-8,方程有两个相等的根t=-1.
②当△=(6+k)2-4>0时,即 k<-8,或k>-4时,
令h(t)=t2-6t+1-kt,由题意可得 h(-1)h(1)=(k+8)(-k-4)<0,解得 k<-8,或 k>-4.
综合①②可得,当k≥-4,或k≤-8 时,关于t的方程g(t)=kt有且只有一个实根.
故所求的实数k的取值范围为(-∞,-8[∪[-4,+∞).
分析:(1)当t=1时,f(x)=(sinx-1)2-4,故当sinx=1时,f(x)有最小值等于-4.
(2)若t∈R,由f(x)=(sinx-t)2+t2-6t+1,分t<-1、-1≤t≤1、t>1三种情况分别求出f(x)的
最小值g(t)的解析式.
(3)由题意可得方程 t2-6t+1-kt=0 在[-1,1]内有且只有一个实根,分△=0和△>0两种情况,分别求得求得
实数k的取值范围,再把得到的实数k的取值范围取并集,即得所求.
点评:本题考查三角函数的恒等变换及化简求值,三角函数的最值,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目