题目内容
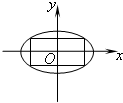椭圆
的内接矩形面积的最大值是________．
12
分析：设出椭圆的内接矩形的一个顶点坐标，表示出面积的表达式，然后求出最大值．
解答：设椭圆上矩形在第一选项内的点的坐标为（3cosθ，2sinθ），θ∈（0，
）
所以椭圆的内接矩形面积S=4×3cosθ•2sinθ=12sin2θ≤12．
故答案为：12．
点评：本题是基础题，考查几何图形的面积的最值的求法，考查计算能力．
分析：设出椭圆的内接矩形的一个顶点坐标，表示出面积的表达式，然后求出最大值．
解答：设椭圆上矩形在第一选项内的点的坐标为（3cosθ，2sinθ），θ∈（0，
）所以椭圆
的内接矩形面积S=4×3cosθ•2sinθ=12sin2θ≤12．故答案为：12．
点评：本题是基础题，考查几何图形的面积的最值的求法，考查计算能力．
练习册系列答案
相关题目
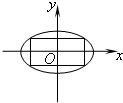椭圆
的内接矩形面积的最大值为________.
=1上,则以P为顶点的椭圆的内接矩形PABC的面积是________________.