题目内容
7.设函数f(x)=x2-ax+a+3,g(x)=x-a.(1)若不存在x0∈R,使得f(x0)<0与g(x0)<0同时成立,求实数a的取值范围;
(2)设h(x)=f(x)+2x|x-a|+ax-a-3,若不等式4≤h(x)≤16在x∈[1,2]上恒成立,求实数a的取值范围.
分析 (1)当x>a时,g(x)>0恒成立,显然不存在x0∈(a,+∞),使得f(x0)<0与g(x0)<0同时成立,当x≤a时,则需f(x)≥0在(-∞,a]上恒成立,只需f(x)在(-∞,a]上的最小值大于或等于零即可,利用二次函数的图象性质求最小值并解不等式即可得a的取值范围.
(2)求出函数h(x)=x2+2x|x-a|,由题意知,只需hmin(x)≥4,hmax(x)≤16,利用h(x)在x∈[1,2]上恒递增,可求得a的范围$a≤-\frac{1}{2}$或$a≥\frac{5}{2}$;再对a分$a≥\frac{5}{2}$与$a≤-\frac{1}{2}$两类讨论,即可求得a的取值范围.
解答 解:(1)①若x≤a,则g(x)≤0,此时若不存在x0∈(-∞,a],使得f(x0)<0与g(x0)<0同时成立,需f(x)≥0在(-∞,a]上恒成立,
即x2-ax+a+3≥0在(-∞,a]上恒成立,
需$\left\{\begin{array}{l}{a>0}\\{f(\frac{a}{2})≥0}\end{array}\right.$或$\left\{\begin{array}{l}{a≤0}\\{f(a)≥0}\end{array}\right.$,即$\left\{\begin{array}{l}{a>0}\\{-\frac{{a}^{2}}{4}+a+3≥0}\end{array}\right.$或$\left\{\begin{array}{l}{a≤0}\\{a+3≥0}\end{array}\right.$
解得:-3≤a≤6
②若x>a,则g(x)>0恒成立,显然不存在x0∈(a,+∞),使得f(x0)<0与g(x0)<0同时成立,此时a∈R
综上所述,若不存在x0∈R,使得f(x0)<0与g(x0)<0同时成立,实数a的取值范围是[-3,6].
(2)∵f(x)=x2-ax+a+3,
∴h(x)=f(x)+2x|x-a|+ax-a-3=x2+2x|x-a|=$\left\{\begin{array}{l}-(x-a)^{2}+{a}^{2},x≤a\\ 3(x-\frac{a}{3})^{2}-\frac{{a}^{2}}{3},x>a\end{array}\right.$,
当a≥0时,h(x)在(-∞,a)和(a,+∞)上均递增;
当a<0时(如图),h(x)在(-∞,a)和$(\frac{a}{3},+∞)$上递增,在在$(a,\frac{a}{3})$上递减,
由题意知,只需hmin(x)≥4,hmax(x)≤16,
首先,由(Ⅰ)可知,h(x)在x∈[1,2]上恒递增,
则hmin(x)=f(1)=1+2|1-a|≥4,解得$a≤-\frac{1}{2}$或$a≥\frac{5}{2}$;
其次,当$a≥\frac{5}{2}$时,f(x)在R上递增,
故hmax(x)=h(2)=4a-4≤16,解得$\frac{5}{2}≤a≤5$;
当$a≤-\frac{1}{2}$时,h(x)在[1,2]上递增,
故hmax(x)=h(2)=12-4a≤16,解得$-1≤a≤-\frac{1}{2}$.
综上:$-1≤a≤-\frac{1}{2}$或$\frac{5}{2}≤a≤5$.
点评 本题考查函数单调性的判断与证明,着重考查分类讨论思想与数形结合思想、等价转化思想的综合应用,是难题.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案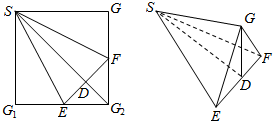 如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3中点,D是EF与SG2的交点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体G-SEF中必有( )
如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3中点,D是EF与SG2的交点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体G-SEF中必有( )| A. | SD⊥平面EFG | B. | SE⊥GF | C. | EF⊥平面SEG | D. | SE⊥SF |
| A. | 12 | B. | 60 | C. | 360 | D. | 2520 |
| A. | (-2,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
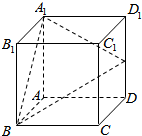 如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.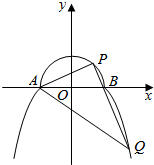 如图所示,曲线C由部分椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1所在椭圆的离心率为$\frac{\sqrt{2}}{2}$,
如图所示,曲线C由部分椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1所在椭圆的离心率为$\frac{\sqrt{2}}{2}$,