题目内容
若x1、x2(x1≠x2)是函数f(x)=ax3+bx2-a2x(a>0)的两个极值点.(1)若
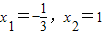 ,求函数f(x)的解析式;
,求函数f(x)的解析式;(2)若
 ,求b的最大值.
,求b的最大值.
【答案】分析:(1)对f(x)进行求导,根据x1、x2(x1≠x2)是函数f(x)的两个极值点可知 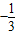 和1是方程3ax2+2bx-a2=0的两根,利用韦达定理建立方程组,解之即可;
和1是方程3ax2+2bx-a2=0的两根,利用韦达定理建立方程组,解之即可;
(2)根据条件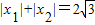 建立b2关于a的函数关系,然后利用导数研究函数的最值即可求出b的最大值
建立b2关于a的函数关系,然后利用导数研究函数的最值即可求出b的最大值
解答:解:(1)∵f(x)=ax3+bx2-a2x(a>0),∴f′(x)=3ax2+2bx-a2(a>0)
依题意有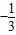 和1是方程3ax2+2bx-a2=0的两根
和1是方程3ax2+2bx-a2=0的两根
∴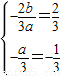 解得
解得 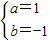 ,∴f(x)=x3-x2-x.(经检验,适合).
,∴f(x)=x3-x2-x.(经检验,适合).
(2)∵f′(x)=3ax2+2bx-a2(a>0)
依题意,x1,x2是方程f′(x)=0的两个根,∵x1x2=-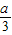 <0且
<0且 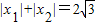 ,
,
∴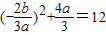 ,∴b2=3a2(9-a)
,∴b2=3a2(9-a)
∵b2≥0∴0<a≤9.
设p(a)=3a2(9-a),则p'(a)=54a-9a2.
由p′(a)>0得0<a<6,由p′(a)<0得a>6.
即函数p(a)在区间(0,6]上是增函数,在区间[6,9]上是减函数,
∴当a=6时,p(a)有极大值为324,∴p(a)在(0,9]上的最大值是324,
∴b的最大值为18.
点评:考查学生会用待定系数法求函数解析式,会利用导数研究函数的极值.
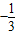 和1是方程3ax2+2bx-a2=0的两根,利用韦达定理建立方程组,解之即可;
和1是方程3ax2+2bx-a2=0的两根,利用韦达定理建立方程组,解之即可;(2)根据条件
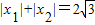 建立b2关于a的函数关系,然后利用导数研究函数的最值即可求出b的最大值
建立b2关于a的函数关系,然后利用导数研究函数的最值即可求出b的最大值解答:解:(1)∵f(x)=ax3+bx2-a2x(a>0),∴f′(x)=3ax2+2bx-a2(a>0)
依题意有
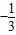 和1是方程3ax2+2bx-a2=0的两根
和1是方程3ax2+2bx-a2=0的两根∴
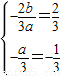 解得
解得 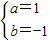 ,∴f(x)=x3-x2-x.(经检验,适合).
,∴f(x)=x3-x2-x.(经检验,适合).(2)∵f′(x)=3ax2+2bx-a2(a>0)
依题意,x1,x2是方程f′(x)=0的两个根,∵x1x2=-
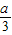 <0且
<0且 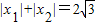 ,
,∴
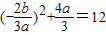 ,∴b2=3a2(9-a)
,∴b2=3a2(9-a)∵b2≥0∴0<a≤9.
设p(a)=3a2(9-a),则p'(a)=54a-9a2.
由p′(a)>0得0<a<6,由p′(a)<0得a>6.
即函数p(a)在区间(0,6]上是增函数,在区间[6,9]上是减函数,
∴当a=6时,p(a)有极大值为324,∴p(a)在(0,9]上的最大值是324,
∴b的最大值为18.
点评:考查学生会用待定系数法求函数解析式,会利用导数研究函数的极值.

练习册系列答案
相关题目