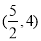题目内容
14.若抛物线y2=2px(p>0)的准线经过双曲线x2-y2=1的左焦点,则p=( )| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 分别求得抛物线y2=2px(p>0)的准线和双曲线x2-y2=1的左焦点,解方程即可得到p.
解答 解:抛物线y2=2px(p>0)的准线为x=-$\frac{p}{2}$,
双曲线x2-y2=1的左焦点为(-$\sqrt{2}$,0),
则由题意可得$\frac{p}{2}$=$\sqrt{2}$,
可得p=2$\sqrt{2}$.
故选D.
点评 本题考查双曲线和抛物线的方程和性质,主要考查抛物线的准线,属于基础题.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
9.抛物线y=x2的准线方程是( )
| A. | y=-$\frac{1}{4}$ | B. | y=$\frac{1}{4}$ | C. | x=-$\frac{1}{4}$ | D. | x=$\frac{1}{4}$ |
2.已知a=π3,b=3π,c=eπ,则a、b、c的大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | b>a>c |
 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把图象上所有的点向右平移1个单位,得到函数
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把图象上所有的点向右平移1个单位,得到函数 的图象,则函数
的图象,则函数 的单调递减区间是( )
的单调递减区间是( ) B.
B.
 D.
D.
 和
和 所围成的封闭曲线如图所示,给定点
所围成的封闭曲线如图所示,给定点 ,若在此封闭曲线上恰有三对不同的点,满足每一对点关于点
,若在此封闭曲线上恰有三对不同的点,满足每一对点关于点 对称,则实数
对称,则实数 的取值范围是( )
的取值范围是( )
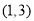 B.
B. C.
C.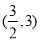 D.
D.