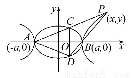
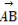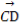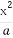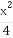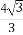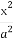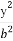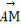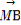题目内容
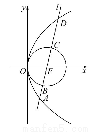
已知平面内一动点P到点F(1,0)的距离与点P到y轴的距离的差等于1.
(1)求动点P的轨迹C的方程.
(2)过点F作两条斜率存在且互相垂直的直线l1,l2,设l1与轨迹C相交于点A,B,l2与轨迹C相交于点D,E,求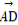 ·
·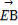 的最小值.
的最小值.
(1) y2=4x(x≥0)和y=0(x<0) (2) 16
【解析】(1)设动点P的坐标为(x,y),由题意得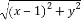 -|x|=1.化简得y2=2x+2|x|,
-|x|=1.化简得y2=2x+2|x|,
当x≥0时,y2=4x;当x<0时,y=0.
所以动点P的轨迹C的方程为
y2=4x(x≥0)和y=0(x<0).
(2)由题意知,直线l1的斜率存在且不为0,设为k,则l1的方程为y=k(x-1).
由 得k2x2-(2k2+4)x+k2=0.
得k2x2-(2k2+4)x+k2=0.
设A(x1,y1),B(x2,y2),则x1,x2是上述方程的两个实根,于是x1+x2=2+ ,x1x2=1.
,x1x2=1.
因为l1⊥l2,所以l2的斜率为-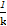 .
.
设D(x3,y3),E(x4, y4),
则同理可得x3+x4=2+4k2,x3x4=1.
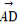 ·
·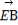 =(
=(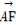 +
+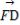 )·(
)·(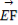 +
+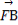 )
)
=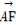 ·
·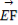 +
+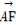 ·
·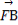 +
+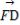 ·
·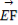 +
+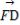 ·
·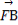
=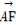 ·
·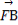 +
+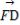 ·
·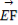 =|
=|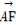 |·|
|·|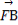 |+|
|+|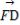 |·|
|·|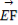 |
|
=(x1+1)(x2+1)+(x3+1)(x4+1)
=x1x2+(x1+x2)+1+x3x4+(x3+x4)+1
=1+(2+ )+1+1+(2+4k2)+1
)+1+1+(2+4k2)+1
=8+4(k2+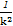 )≥8+4×2
)≥8+4×2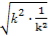 =16.
=16.
故当且仅当k2=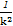 ,即k=±1时,
,即k=±1时,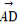 ·
·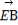 取最小值16.
取最小值16.

练习册系列答案
相关题目