题目内容

已知条件P：函数y=log_cx在（0，+∞）上为单调递减函数；条件Q：不等式x+|x-2c|＞1的解集为R．如果P是Q的充分不必要条件，则实数c需满足的条件是________．

$\text{[math]}$ ≤c＜1
分析：由题设条件知，应先对条件P与条件Q进行等价转化，解出其成立的参数范围，再根据P是Q的充分不必要条件判断出实数c需满足的条件，得到答案
解答：

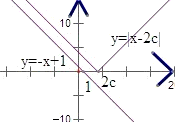
解：由题意，若条件P：函数y=log_cx在（0，+∞）上为单调递减函数；是真命题，则有0＜c＜1；
若条件Q：不等式x+|x-2c|＞1的解集为R是真命题，则有|x-2c|＞1-x恒成立，令y=|x-2c|，y=1-x，如右图，知，2c≥1，即c≥ $\text{[math]}$
又P是Q的充分不必要条件，可得 $\text{[math]}$ ≤c＜1
故答案为 $\text{[math]}$ ≤c＜1
点评：本题考查命题的真假判断与应用，解题的关键是将两个命题的条件进行正确化简，以及理解P是Q的充分不必要条件，由于本题不等式x+|x-2c|＞1的解集为R的转化不容易用文字说明清楚，故采取了图形法作辅助判断，这是解本题的重点，本题难点是理解P是Q的充分不必要条件，本题考查了推理判断的能力，及以形助数的思想，是对命题进行考查的重要题型，题后要注意总结做题的规律，尤其是把不等式恒成立的问题转化为图形的位置关系问题来解决技巧．