题目内容
 选修4--1:几何证明选讲
选修4--1:几何证明选讲如图,D为△ABC的BC边上的一点,⊙O1经过点B、D,交AB于另一点E,⊙O2经过点C、D,交AC于另一点F,⊙O1、⊙O2交于点G.求证:
(1)∠BAC+∠EGF=180°;
(2)∠EAG=∠EFG.
分析:(1)连接GD,由圆内接四边形的性质,可得∠EGD与∠B互补,∠FGD与∠C互补,从而∠EGD+∠B+∠FGD+∠C=360°,结合周角也等于360°,得到∠B+∠C=∠EGF,最后结合三角形内角和定理,得到∠BAC+∠EGF=180°.
(2)由(1)的结论,得到四边形AEGF是圆内接内接四边形,结合同弧所对的圆周角相等,得到∠EAG=∠EFG.
(2)由(1)的结论,得到四边形AEGF是圆内接内接四边形,结合同弧所对的圆周角相等,得到∠EAG=∠EFG.
解答:解:(1)连接GD,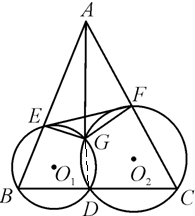
∵四边形BDGE是圆内接四边形,
∴∠EGD+∠B=180°,同理可得∠FGD+∠C=180°,
∴∠EGD+∠B+∠FGD+∠C=360°,
∵∠EGD+∠FGD+∠EGF=360°,
∴∠B+∠C=∠EGF
∵△ABC中,∠B+∠C+∠BAC=180°
∴∠BAC+∠EGF=180°.
(2)∵四边形AEGF中,∠BAC+∠EGF=180°.
∴四边形AEGF是圆内接内接四边形,
设外接圆为圆M,则圆M中∠EAG和∠EFG同对弧EG
∴∠EAG=∠EFG.

∵四边形BDGE是圆内接四边形,
∴∠EGD+∠B=180°,同理可得∠FGD+∠C=180°,
∴∠EGD+∠B+∠FGD+∠C=360°,
∵∠EGD+∠FGD+∠EGF=360°,
∴∠B+∠C=∠EGF
∵△ABC中,∠B+∠C+∠BAC=180°
∴∠BAC+∠EGF=180°.
(2)∵四边形AEGF中,∠BAC+∠EGF=180°.
∴四边形AEGF是圆内接内接四边形,
设外接圆为圆M,则圆M中∠EAG和∠EFG同对弧EG
∴∠EAG=∠EFG.
点评:本题以三角形内角和与圆内接四边形为例,考查了与圆有关的角相等和角互补的证明,属于基础题.

练习册系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 (2013•海口二模)选修4-1:几何证明选讲
(2013•海口二模)选修4-1:几何证明选讲 (2012•徐州模拟)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,
(2012•徐州模拟)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答, 选修4-1:几何证明选讲
选修4-1:几何证明选讲 (2013•南通一模)选修4-1:几何证明选讲
(2013•南通一模)选修4-1:几何证明选讲