题目内容

16．比较大小：logmtnt与logmn（n＞m＞1，t＞1）

分析 n＞m＞1，t＞1，可得logmtnt＞0，logmn＞0．利用对数换底公式可得：logmtnt=$\frac{lo{g}_{t}^{n}+1}{lo{g}_{t}^{m}+1}$，$\frac{lo{g}_{t}^{n}}{lo{g}_{t}^{m}}$=$lo{g}_{m}^{n}$，利用不等式的性质即可得出．

解答 解：∵n＞m＞1，t＞1，∴logmtnt＞0，logmn＞0．
∴logmtnt=$\frac{lo{g}_{t}^{n}+1}{lo{g}_{t}^{m}+1}$＜$\frac{lo{g}_{t}^{n}}{lo{g}_{t}^{m}}$=$lo{g}_{m}^{n}$，
∴logmtnt＜logmn．

点评 本题考查了对数的运算性质、换底公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
6．已知数列{an}为等比数列．
（1）a52=a3•a7是否成立？a52=a1•a9成立吗？为什么？
（2）an2=an-1•an+1（n＞1）是否成立？你据此能得到什么结论？
（3）an2=an-k•an+k（n＞k＞0）是否成立？你又能得到什么结论？
7．已知集合A={y|y＞a+3或y＜a}，B={2≤y≤4}，若A∩B≠∅，求实数a的取值范围．
4．证明：$\frac{tanθ（1+sinθ）+sinθ}{tanθ（1+sinθ）-sinθ}$=$\frac{tanθ+sinθ}{tanθsinθ}$．
11．直线y=x-$\frac{1}{2}$被椭圆x2+4y2=4截得的弦长为$\frac{2\sqrt{38}}{5}$．
1．已知函数f（x）=lnx+mx2（m∈R）．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）若m=0，A（a，f（a））、B（b，f（b））是函数f（x）图象上不同的两点，且a＞b＞0，f′（x）为f（x）的导函数，求证：f′（$\frac{a+b}{2}$）＜$\frac{f（a）-f（b）}{a-b}$＜f′（b）；
（Ⅲ）求证：$\frac{2}{3}+\frac{2}{5}+\frac{2}{7}+…+\frac{2}{2n+1}$＜ln（n+1）＜1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}$（n∈N*）．
8．已知函数y=（x-a）2+1，-2≤x≤2，求函数y的最值．
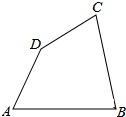5．如图，凸四边形ABCD，求作一个三角形，使得该三角形的面积和凸四边形ABCD的面积相等．
6．若log4x=3，则log16x等于（　　）
A．$\frac{3}{2}$B．9C．$\sqrt{3}$D．64

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网