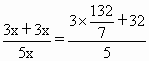题目内容
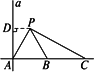
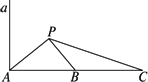
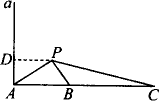
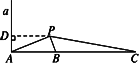
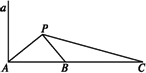
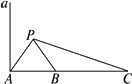
如图所示,a是海面上一条南北方向的海防警戒线,在a上点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20 km处和54 km处.某时刻,监测点B收到发自静止目标P的一个声波,8 s后监测点A、20 s后监测点C相继收到这一信号.在当时气象条件下,声波在水中的传播速度是1.5 km/s.

(1)设A到P的距离为x km,用x表示B,C到P的距离,并求x的值;
(2)求静止目标P到海防警戒线a的距离(结果精确到0.01 km).
答案:
解析:
解析:
|
答:静止目标P到海防警戒线a的距离约为17.71 km. 解:(1)依题意,PA-PB=1.5×8=12(km),PC-PB=1.5×20=30(km). 因此,PB=(x-12)km,PC=(18+x)km. 在△PAB中,AB=20 km, cos∠PAB= 同理,在△PAC中,cos∠PAC= 由于cos∠PAB=cos∠PAC, 即 解得x= (2)作PD⊥a,垂足为D.
在Rt△PDA中, PD=PAcos∠APD=PAcos∠PAB =x· ≈17.71(km). 思路分析:这是一实际应用问题,通过阅读题意,发现求x就是解△PAB和△PBC,所以可利用余弦定理分别列出边和角的关系式,其中∠PAB=∠PAC. |

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目