题目内容
6.已知定义在R上的偶函数f(x)满足,当x≥0时,f(x)=x3+x2,则不等式f(x-1)>f(2x)的解集为( )| A. | (-3,1) | B. | (-1,$\frac{1}{3}$) | C. | (-∞,-1)∪($\frac{1}{3}$,+∞) | D. | (-∞,-$\frac{1}{3}$)∪(1,+∞) |
分析 根据导数判断函数的单调性,利用函数奇偶性和单调性之间的关系将不等式进行转化即可.
解答 解:当x≥0时,f(x)=x3+x2,函数的导数f′(x)=3x2+2x=x(3x+2)≥0,即此时函数为增函数,
∵函数f(x)是偶函数,
∴不等式f(x-1)>f(2x)等价为不等式f(|x-1|)>f(|2x|),
即|x-1|>|2x|,
平方得x2-2x+1>4x2,
即3x2+2x-1<0,
即(x+1)(3x-1)<0,
解得-1<x<$\frac{1}{3}$,
故不等式的解集为(-1,$\frac{1}{3}$),
故选:B
点评 本题主要考查不等式的求解,根据导数,判断函数的单调性,利用奇偶性和单调性之间的关系将不等式进行转化是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.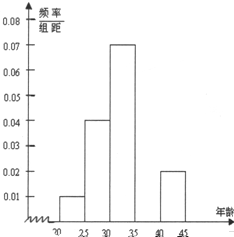 某手机销售商对某市市民进行手机品牌认可度的调查,在已购买某品牌手机的500名市民中,随机抽样100名,按年龄进行统计的频率分布表和频率分布直方图如下:
某手机销售商对某市市民进行手机品牌认可度的调查,在已购买某品牌手机的500名市民中,随机抽样100名,按年龄进行统计的频率分布表和频率分布直方图如下:
(1)频率分布表中①②应填什么数?补全频率分布直方图,并根据频率分布直方图估计这500名市民的平均年龄;
(2)在抽出的这100市民中,按分层抽样抽取20人参加宣传活动,从20人中随机选取2人各赠送一部手机,设这两名市民中年龄低于30岁的人数为X,求X的分布列及数学期望.
 某手机销售商对某市市民进行手机品牌认可度的调查,在已购买某品牌手机的500名市民中,随机抽样100名,按年龄进行统计的频率分布表和频率分布直方图如下:
某手机销售商对某市市民进行手机品牌认可度的调查,在已购买某品牌手机的500名市民中,随机抽样100名,按年龄进行统计的频率分布表和频率分布直方图如下:| 分组(岁) | 频数 | 频率 |
| [20,25) | 5 | 0.05 |
| [25,30) | 20 | 0.2 |
| [30,35) | ① | 0.35 |
| [35,40) | 30 | 0.3 |
| [40,45) | 10 | ② |
| 合计 | 100 | 1.0 |
(2)在抽出的这100市民中,按分层抽样抽取20人参加宣传活动,从20人中随机选取2人各赠送一部手机,设这两名市民中年龄低于30岁的人数为X,求X的分布列及数学期望.
 某校高三年级在某次模拟考试中,从全年级400名学生中选出40名学生的数学成绩制成了平率分布直方图如图所示.
某校高三年级在某次模拟考试中,从全年级400名学生中选出40名学生的数学成绩制成了平率分布直方图如图所示. 在中央军委的决策部署下,全军广大青年官兵广泛开展“强素质,练打赢,当尖兵”的技能比武大赛,某海军陆战队A队现有9名侦察兵去参加军区举办的“超级战士”大赛,该活动有A、B、C三个比赛项目,恰好各有3名战士进入三个比赛项目.
在中央军委的决策部署下,全军广大青年官兵广泛开展“强素质,练打赢,当尖兵”的技能比武大赛,某海军陆战队A队现有9名侦察兵去参加军区举办的“超级战士”大赛,该活动有A、B、C三个比赛项目,恰好各有3名战士进入三个比赛项目.