题目内容
14.已知函数f(x)=2ax2+bx-3a+1,当x∈[-4,4]时,f(x)≥0恒成立,则5a+b最值为最大值为$\frac{17}{21}$;最小值为-$\frac{1}{3}$.分析 由题意,f(0)≥0成立,所以a≤$\frac{1}{3}$,再分类讨论,利用线性规划知识求解,即可求出5a+b的最小值.
解答 
 解:由题意,f(0)≥0成立,所以a≤$\frac{1}{3}$.
解:由题意,f(0)≥0成立,所以a≤$\frac{1}{3}$.
①0<a≤$\frac{1}{3}$时,则问题等价于$\left\{\begin{array}{l}{-\frac{b}{4a}≤-4}\\{f(-4)≥0}\end{array}\right.$(1)或$\left\{\begin{array}{l}{-\frac{b}{4a}≥4}\\{f(4)≥0}\end{array}\right.$(2)或$f(-\frac{b}{4a})≥0$(3)
(1)$\left\{\begin{array}{l}{16a-b≤0}\\{29a-4b+1≥0}\end{array}\right.$,对应的区域如图所示,
由图知,直线z=5a+b经过点O(0,0)时,取得最小值0;
直线z=5a+b经过点($\frac{1}{35}$,$\frac{16}{35}$)时,取得最大值$\frac{21}{35}$;
(2)$\left\{\begin{array}{l}{16a+b≤0\\;}\\{29a+4b+1≥0}\end{array}\right.$对应的区域如图所示,
由图知,直线z=5a+b经过点A($\frac{1}{35}$,-$\frac{16}{35}$)时,取得最小值-$\frac{11}{35}$;
直线z=5a+b经过点O(0,0)时,取得最大值0;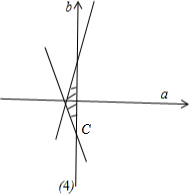

(3)24a2-8a+b2≤0,对应的区域如图所示,
由图知,直线z=5a+b经过点B($\frac{1}{21}$,-$\frac{12}{21}$)时,取得最小值-$\frac{1}{3}$;
直线z=5a+b经过点($\frac{1}{21}$,$\frac{12}{21}$)时,取得最大值$\frac{17}{21}$;
②a≤0时,问题等价于$\left\{\begin{array}{l}{f(-4)≥0}\\{f(4)≥0}\end{array}\right.$,$\left\{\begin{array}{l}{29a-4b+1≥0}\\{29a+4b+1≥0}\end{array}\right.$,对应的区域如图所示,
由图知,直线z=5a+b经过点C(0,-$\frac{1}{4}$)时,取得最小值-$\frac{1}{4}$,
直线z=5a+b经过点C(0,$\frac{1}{4}$)时,取得最大值$\frac{1}{4}$;
综上,a=$\frac{1}{21}$,b=$\frac{12}{21}$时,取得最大值$\frac{17}{21}$.
a=$\frac{1}{21}$,b=-$\frac{12}{21}$时,取得最小值-$\frac{1}{3}$.
故答案为,:5a+b最大值为$\frac{17}{21}$;最小值为-$\frac{1}{3}$.
点评 本题考查的是不等式以及线性规划,考查学生分析解决问题的能力,考查学生的计算能力,属于难题.

 如图,在地面上共线的三点A,B,C处测得一建筑物的仰角分别为30°,45°,60°,且AB=BC=60m,则建筑物的高度为( )
如图,在地面上共线的三点A,B,C处测得一建筑物的仰角分别为30°,45°,60°,且AB=BC=60m,则建筑物的高度为( )| A. | 15$\sqrt{6}$m | B. | 20$\sqrt{6}$m | C. | 25$\sqrt{6}$m | D. | 30$\sqrt{6}$m |
| A. | [-2,3] | B. | [-1,3] | C. | (-2,3] | D. | (-1,3] |
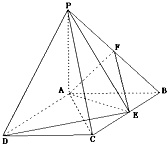 如图四棱锥P-ABCD中PA⊥平面ABCD,底面ABCD是矩形,PA=AB=1,∠PDA=30°,点F是PB的中点,点E在边BC上移动.
如图四棱锥P-ABCD中PA⊥平面ABCD,底面ABCD是矩形,PA=AB=1,∠PDA=30°,点F是PB的中点,点E在边BC上移动.