题目内容
如图,在三棱锥 中,
中, ,
, ,
,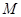 为
为 中点,
中点, 为
为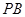 中点,且
中点,且 为正三角形.
为正三角形.

(1)求证: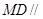 平面
平面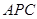 .
.
(2)求证:平面 ⊥平面
⊥平面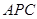 .
.
【答案】
(1)只需证MD//AP;(2)只需证BC⊥平面APC。
【解析】

试题分析:(1)∵M为AB中点,D为PB中点,
∴MD//AP,
又MD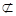 平面ABC, AP
平面ABC, AP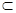 平面ABC
平面ABC
∴MD//平面APC
(2)∵△PMB为正三角形,且D为PB中点,
∴MD⊥PB.
又由(Ⅰ)知MD//AP,
∴AP⊥PB.
又已知AP⊥PC,PB∩PC=P
∴AP⊥平面PBC,而BC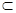 平面PBC,
平面PBC,
∴AP⊥BC,
又AC⊥BC,而AP∩AC="A,"
∴BC⊥平面APC,
又BC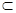 平面ABC
平面ABC
∴平面ABC⊥平面PAC
考点:线面平行的判定定理;面面垂直的判定定理;线面垂直的判定定理。
点评:证明线面平行的常用方法:①定义:若一条直线和一个平面没有公共点,则它们平行;
②线线平行Þ线面平行
若平面外的一条直线平行于平面内的一条直线,则它与这个平面平行。
 即
即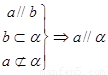
③面面平行Þ线面平行
若两平面平行,则其中一个平面内的任一条直线平行于另一个平面。
 即
即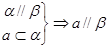

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
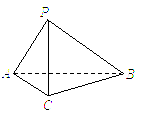 如图,在三棱锥
如图,在三棱锥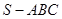 中,侧面
中,侧面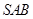 与侧面
与侧面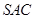 均为等边三角形,
均为等边三角形,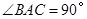 ,
,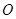 为
为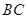 中点.
中点.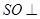 平面
平面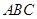 ;
;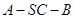 的余弦值. (本题12分)
的余弦值. (本题12分)
 中,
中, 两两垂直且相等,过
两两垂直且相等,过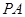 的中点
的中点 作平面
作平面 ∥
∥ ,且
,且 于
于 ,交
,交 的延长线于
的延长线于 .
. 平面
平面 ;
; ,求二面角
,求二面角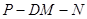 的余弦值.
的余弦值.
 中,已知点
中,已知点 、
、 、
、 分别为棱
分别为棱 、
、 、
、 的中点.
的中点. ∥平面
∥平面 ;
; ,
, ,求证:平面
,求证:平面 ⊥平面
⊥平面
 中,
中, ,
, 为
为 中点。(1)求证:
中点。(1)求证: 平面
平面
 上是否存在一点
上是否存在一点 ,使二面角
,使二面角 的平面角的余弦值为
的平面角的余弦值为 ?若存在,确定
?若存在,确定