题目内容
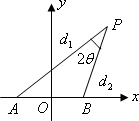
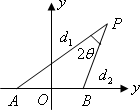
设动点P到点A(-1,0)和B(1,0)的距离分别为d1和d2,∠APB=2θ,且存在常数λ(0<λ<1),使得d1d2sin2θ=λ.(1)证明:动点P的轨迹C为双曲线,并求出C的方程;
(2)过点B作直线双曲线C的右支于M,N两点,试确定λ的范围,使
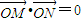 ,其中点O为坐标原点.
,其中点O为坐标原点.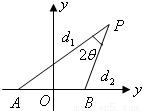
【答案】分析:(1)首先利用余弦定理写出d1和d2的等量关系式,然后把它变形为(d1-d2)2=*的形式,即|d1-d2|=*的形式,此时满足双曲线的定义,则问题得证,最后由双曲线的标准方程形式即可写出其方程.
(2)首先根据直线MN是否垂直于x轴进行讨论,若直线MN垂直于x轴,则直线方程为x=1,又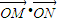 =0可得M、N的坐标,代入双曲线方程即得λ的值;若直线MN不垂直于x轴,则设其点斜式方程,并与双曲线方程联立方程组,可消y得x的一元二次方程,再由根与系数的关系用k与λ的代数式表示出x1+x2和x1x2,进而由
=0可得M、N的坐标,代入双曲线方程即得λ的值;若直线MN不垂直于x轴,则设其点斜式方程,并与双曲线方程联立方程组,可消y得x的一元二次方程,再由根与系数的关系用k与λ的代数式表示出x1+x2和x1x2,进而由 =0及x1+x2>0,x1x2>0通过整理消去k得到λ的不等式,此时解不等式即可,最后把两种情况综合之.
=0及x1+x2>0,x1x2>0通过整理消去k得到λ的不等式,此时解不等式即可,最后把两种情况综合之.
解答:(1)证明:在△PAB中,|AB|=2,即22=d12+d22-2d1d2cos2θ,4=(d1-d2)2+4d1d2sin2θ,
即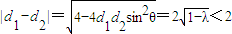 (常数),
(常数),
所以点P的轨迹C是以A,B为焦点,实轴长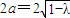 的双曲线.
的双曲线.
又b2=1-(1-λ),所以C的方程为: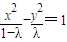 .
.
(2)解:设M(x1,y1),N(x2,y2)
①当MN垂直于x轴时,MN的方程为x=1,M(1,1),N(1,-1)在双曲线上.
即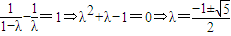 ,因为0<λ<1,所以
,因为0<λ<1,所以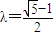 .
.
②当MN不垂直于x轴时,设MN的方程为y=k(x-1).
由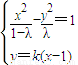 得:[λ-(1-λ)k2]x2+2(1-λ)k2x-(1-λ)(k2+λ)=0,
得:[λ-(1-λ)k2]x2+2(1-λ)k2x-(1-λ)(k2+λ)=0,
由题意知:[λ-(1-λ)k2]≠0,
所以 ,
,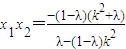 .
.
于是: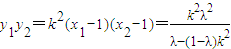 .
.
因为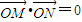 ,且M,N在双曲线右支上,所以
,且M,N在双曲线右支上,所以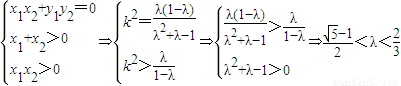 .
.
由①②知,λ的取值范围是: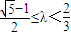 .
.
点评:本题考查双曲线的定义、标准方程及直线与圆锥曲线的位置关系,综合性强,字母运算量大,且需分类讨论.
(2)首先根据直线MN是否垂直于x轴进行讨论,若直线MN垂直于x轴,则直线方程为x=1,又
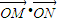 =0可得M、N的坐标,代入双曲线方程即得λ的值;若直线MN不垂直于x轴,则设其点斜式方程,并与双曲线方程联立方程组,可消y得x的一元二次方程,再由根与系数的关系用k与λ的代数式表示出x1+x2和x1x2,进而由
=0可得M、N的坐标,代入双曲线方程即得λ的值;若直线MN不垂直于x轴,则设其点斜式方程,并与双曲线方程联立方程组,可消y得x的一元二次方程,再由根与系数的关系用k与λ的代数式表示出x1+x2和x1x2,进而由 =0及x1+x2>0,x1x2>0通过整理消去k得到λ的不等式,此时解不等式即可,最后把两种情况综合之.
=0及x1+x2>0,x1x2>0通过整理消去k得到λ的不等式,此时解不等式即可,最后把两种情况综合之.解答:(1)证明:在△PAB中,|AB|=2,即22=d12+d22-2d1d2cos2θ,4=(d1-d2)2+4d1d2sin2θ,
即
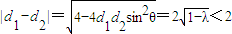 (常数),
(常数),所以点P的轨迹C是以A,B为焦点,实轴长
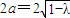 的双曲线.
的双曲线.又b2=1-(1-λ),所以C的方程为:
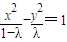 .
.(2)解:设M(x1,y1),N(x2,y2)
①当MN垂直于x轴时,MN的方程为x=1,M(1,1),N(1,-1)在双曲线上.
即
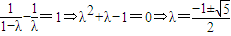 ,因为0<λ<1,所以
,因为0<λ<1,所以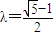 .
.②当MN不垂直于x轴时,设MN的方程为y=k(x-1).
由
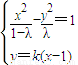 得:[λ-(1-λ)k2]x2+2(1-λ)k2x-(1-λ)(k2+λ)=0,
得:[λ-(1-λ)k2]x2+2(1-λ)k2x-(1-λ)(k2+λ)=0,由题意知:[λ-(1-λ)k2]≠0,
所以
 ,
,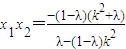 .
.于是:
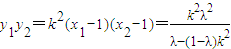 .
.因为
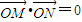 ,且M,N在双曲线右支上,所以
,且M,N在双曲线右支上,所以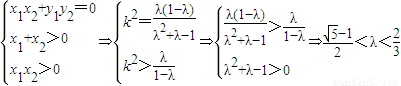 .
.由①②知,λ的取值范围是:
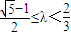 .
.点评:本题考查双曲线的定义、标准方程及直线与圆锥曲线的位置关系,综合性强,字母运算量大,且需分类讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 设动点P到点A(-1,0)和B(1,0)的距离分别为d1和d2,∠APB=2θ,且存在常数λ(0<λ<1),使得d1d2sin2θ=λ.
设动点P到点A(-1,0)和B(1,0)的距离分别为d1和d2,∠APB=2θ,且存在常数λ(0<λ<1),使得d1d2sin2θ=λ.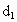 和
和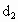 ,∠APB=2θ,且存在常数λ(0<λ<1),使得
,∠APB=2θ,且存在常数λ(0<λ<1),使得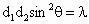 .
.
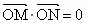 ,其中点O为坐标原点.
,其中点O为坐标原点.