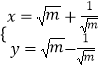题目内容
【题目】设函数f（x）=a（x﹣1）2﹣xe2﹣x ．
（Ⅰ）若曲线y=f（x）在点（2，f（2））处的切线与x轴平行，求a的值；
（Ⅱ）若 
，求f（x）的单调区间．
【答案】解：（I）因为f（x）=a（x﹣1）2﹣xe2﹣x，
所以f'（x）=2a（x﹣1）﹣（e2﹣x﹣xe2﹣x）．因为f（x）在点（2，f（2））处的切线与x轴平行，所以f′（2）=0，1+2a=0，a=﹣ 
．…
（II）因为f′（x）=（x﹣1）（e2﹣x+2a），
⑴所以f′（x）＞0，解得：x＞1，f′（x）＜0，解得：x＜1
所以函数f（x）的单调递增区间为（1，+∞），函数f（x）的单调递减区间为（﹣∞，1）；
⑵当﹣ 
＜a＜0时，
令f′（x）=0，得x1=1，x2=2﹣ln（﹣2a），且x2﹣x1=1﹣ln（﹣2a）＞0．
当x变化时，f′（x），f（x）的变化情况如下表：
x | （﹣∞，1） | 1 | （1，2﹣ln（﹣2a）） | 2﹣ln（﹣2a） | （2﹣ln（﹣2a），+∞） |
f′（x） | ﹣ | 0 | + | 0 | ﹣ |
f（x） | 极小值 | 极大值 |
所以函数f（x）的单调递增区间为（1，2﹣ln（﹣2a）），
函数f（x）的单调递减区间为（﹣∞，1），（2﹣ln（﹣2a），+∞）；
综上所述：
当a≥0时，函数f（x）的单调递增区间为（1，+∞），函数f（x）的单调递减区间为（﹣∞，1）；
当﹣ ＜a＜0时，函数f（x）的单调递增区间为（1，2﹣ln（﹣2a）），
函数f（x）的单调递减区间为：（﹣∞，1），（2﹣ln（﹣2a），+∞）．…
【解析】1、( 1 )、求导可得因为f（x）在点（2，f（2））处的切线与x轴平行，所以f′（2）=0，1+2a=0，a=﹣ .
（2）、由第I问可得f′（x）＞0，解得：x＞1，f′（x）＜0，解得：x＜1所以函数f（x）的单调递增区间为（1，+∞），函数f（x）的单调递减区间为（﹣∞，1）；
2、令f′（x）=0，得x1=1，x2=2﹣ln（﹣2a），且x2﹣x1=1﹣ln（﹣2a）＞0．列图表可得当a≥0时，函数f（x）的单调递增区间为（1，+∞），函数f（x）的单调递减区间为（﹣∞，1）；当﹣ ＜a＜0时，函数f（x）的单调递增区间为（1，2﹣ln（﹣2a）），
函数f（x）的单调递减区间为：（﹣∞，1），（2﹣ln（﹣2a），+∞）。
