题目内容
已知函数f(x)=3x2+2x+1,若
f(x)dx=2f(a)(a>0)成立,则a=______.
| ∫ | 1-1 |
由∫-11f(x)dx=∫-11(3x2+2x+1)dx
=(x3+x2+x)|-11=4=2f(a),
得f(a)=3a2+2a+1=2,
解得a=-1或
.
∵a>0.∴a=
故答案为:
.
=(x3+x2+x)|-11=4=2f(a),
得f(a)=3a2+2a+1=2,
解得a=-1或
| 1 |
| 3 |
∵a>0.∴a=
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |

练习册系列答案
相关题目

 ,
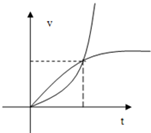
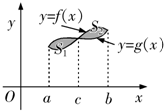
,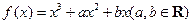 的图象,如图所示,它与直线
的图象,如图所示,它与直线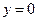 在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为
在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为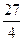 ,则
,则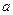 的值为 .
的值为 .