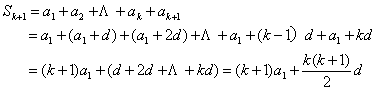题目内容
某学生在证明等差数列前n项和公式时,证法如下:(1)当n=1时,S1=a1显然成立.
(2)假设n=k时,公式成立,即
Sk=ka1+![]() ,
,
当n=k+1时,
Sk+1=a1+a2+…+ak+ak+1
=a1+(a1+d)+(a1+2d)+…+a1+(k-1)d+a1+kd
=(k+1)a1+(d+2d+…+kd)
=(k+1)a1+![]() d
d
=(k+1)a1+![]() d.
d.
∴n=k+1时公式成立.
∴由(1)(2)可知对n∈N+,公式成立.
以上证明错误的是( )
A.当n取第一个值1时,证明不对
B.归纳假设写法不对
C.从n=k到n=k+1的推理中未用归纳假设
D.从n=k到n=k+1的推理有错误
思路解析:在第(2)步证明中,归纳假设未用到.
答案:C

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目