题目内容
已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=x(x-2)。
(1)求出函数f(x)的解析式;
(2)画出函数f(x)的图像。
(1)求出函数f(x)的解析式;
(2)画出函数f(x)的图像。
解:(1)函数f(x)是定义在R上的奇函数,
∴f(-x)=-f(x), ①
f(0)=0, ②
又x>0时,f(x)=x(x-2),
∴当x<0时,有-x>0,
∴f(-x)=(-x)(-x-2)=x(x+2),即f(-x)=x(x+2), ③
由①②③,得函数f(x)的解析式为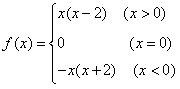 ;
;
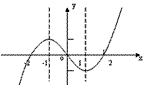
(2)函数的图像见下图:
∴f(-x)=-f(x), ①
f(0)=0, ②
又x>0时,f(x)=x(x-2),
∴当x<0时,有-x>0,
∴f(-x)=(-x)(-x-2)=x(x+2),即f(-x)=x(x+2), ③
由①②③,得函数f(x)的解析式为
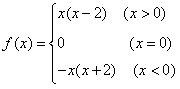 ;
;(2)函数的图像见下图:


练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目