题目内容
将函数y=sin（4x+
）的图象上各点的横坐标伸长为原来的2倍，再向右平移
个单位，得到的函数的图象的一个对称中心为
- A.
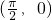
- B.
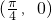
- C.（
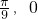） - D.
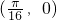
A
分析：把原函数的图象变换后得到函数 y=sin2x 的图象，故所得函数的对称中心为 （
，0），k∈z，由此可得答案．
解答：将函数y=sin（4x+）的图象上各点的横坐标伸长为原来的2倍，可得函数y=sin（2x+）的图象，
再向右平移个单位，得到函数 y=sin[2（x-）+]=sin2x 的图象．
令2x=kπ，可得 x=，k∈z． 故所得函数的对称中心为 （，0），k∈z．
故选A．
点评：本题主要考查函数y=Asin（ωx+∅）的图象变换规律，正弦函数的对称中心，属于中档题．
分析：把原函数的图象变换后得到函数 y=sin2x 的图象，故所得函数的对称中心为 （
，0），k∈z，由此可得答案．解答：将函数y=sin（4x+
）的图象上各点的横坐标伸长为原来的2倍，可得函数y=sin（2x+）的图象，再向右平移
个单位，得到函数 y=sin[2（x-）+]=sin2x 的图象．令2x=kπ，可得 x=
，k∈z． 故所得函数的对称中心为 （，0），k∈z．故选A．
点评：本题主要考查函数y=Asin（ωx+∅）的图象变换规律，正弦函数的对称中心，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
将函数y=sin(2x+
)的图象上各点的纵坐标不变，横坐标伸长到原来的2倍，再向右平移
个单位，所得到的图象解析式是（ ）
| π |
| 4 |
| π |
| 4 |
| A、f（x）=sinx |
| B、f（x）=cosx |
| C、f（x）=sin4x |
| D、f（x）=cos4x |