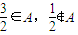题目内容
设不等式|x-2|<m(m∈N+)的解集为A,且| 3 |
| 2 |
| 1 |
| 2 |
(Ⅰ)求m的值;
(Ⅱ)若a,b,c∈R+,且a+b+c=
| m |
| 2 |
| 1 |
| a+b |
| 1 |
| b+c |
| 1 |
| c+a |
分析:(Ⅰ)根据
∈A,
∉A,求出m的范围,结合m∈N+,即可求m的值;
(Ⅱ)利用“1”的代换,结合基本不等式,即可得出结论.
| 3 |
| 2 |
| 1 |
| 2 |
(Ⅱ)利用“1”的代换,结合基本不等式,即可得出结论.
解答:(Ⅰ)解:由
⇒
⇒
<m≤
.--(4分)
∵m∈N+,
∴m=1.--(5分)
(Ⅱ)证明:由(Ⅰ)有:a+b+c=
⇒2a+2b+2c=1(a,b,c∈R+)
又
+
+
=(
+
+
)×1=(
+
+
)(2a+2b+2c)
=(
+
+
)[(a+b)+(b+c)+(c+a)]≥9,
∴
+
+
≥9--(10分)
|
|
| 1 |
| 2 |
| 3 |
| 2 |
∵m∈N+,
∴m=1.--(5分)
(Ⅱ)证明:由(Ⅰ)有:a+b+c=
| 1 |
| 2 |
又
| 1 |
| a+b |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
| 1 |
| b+c |
| 1 |
| c+a |
=(
| 1 |
| a+b |
| 1 |
| b+c |
| 1 |
| c+a |
∴
| 1 |
| a+b |
| 1 |
| b+c |
| 1 |
| c+a |
点评:本题考查绝对值不等式的解法,考查不等式的证明,正确运用“1”的代换,基本不等式,是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目