题目内容
已知函数 
 .
.
(1)当 时,求函数
时,求函数 在点
在点 处的切线方程及函数
处的切线方程及函数 的单调区间.
的单调区间.
(2)设 在
在 上的最小值为
上的最小值为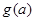 ,求
,求 的解析式
的解析式

 .
.(1)当
 时,求函数
时,求函数 在点
在点 处的切线方程及函数
处的切线方程及函数 的单调区间.
的单调区间.(2)设
 在
在 上的最小值为
上的最小值为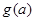 ,求
,求 的解析式
的解析式解: (1) 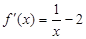 (
(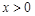 ),
),
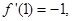
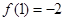
切线方程: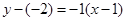
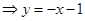
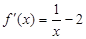 (
(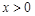 ),
),
①由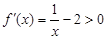 ,得
,得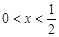
②由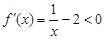 ,得
,得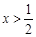
故函数 的单调递增区间为
的单调递增区间为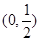 ,单调减区间是
,单调减区间是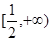 .
.
(2)①当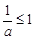 ,即
,即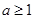 时,函数
时,函数 在区间[1,2]上是减函数,
在区间[1,2]上是减函数,
∴ 的最小值是
的最小值是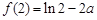 .
.
②当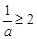 ,即
,即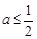 时,函数
时,函数 在区间[1,2]上是增函数,
在区间[1,2]上是增函数,
∴ 的最小值是
的最小值是 .
.
③当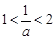 ,即
,即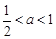 时,函数
时,函数 在
在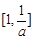 上是增函数,在
上是增函数,在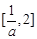 是减函数.
是减函数.
又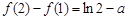 ,
,
∴当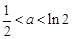 时,最小值是
时,最小值是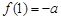 ;
;
当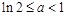 时,最小值为
时,最小值为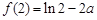 .
.
综上可知,当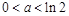 时, 函数
时, 函数 的最小值是
的最小值是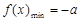 ;当
;当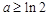 时,函数
时,函数 的最小值是
的最小值是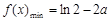 .
.
即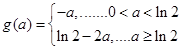 ………………14分
………………14分
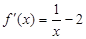 (
(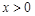 ),
), 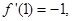
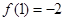
切线方程:
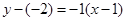
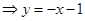
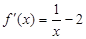 (
(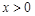 ),
), ①由
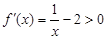 ,得
,得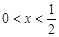
②由
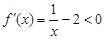 ,得
,得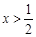
故函数
 的单调递增区间为
的单调递增区间为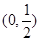 ,单调减区间是
,单调减区间是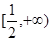 .
. (2)①当
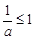 ,即
,即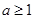 时,函数
时,函数 在区间[1,2]上是减函数,
在区间[1,2]上是减函数,∴
 的最小值是
的最小值是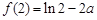 .
. ②当
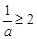 ,即
,即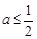 时,函数
时,函数 在区间[1,2]上是增函数,
在区间[1,2]上是增函数,∴
 的最小值是
的最小值是 .
. ③当
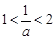 ,即
,即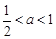 时,函数
时,函数 在
在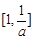 上是增函数,在
上是增函数,在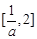 是减函数.
是减函数.又
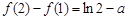 ,
,∴当
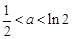 时,最小值是
时,最小值是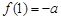 ;
;当
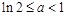 时,最小值为
时,最小值为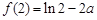 .
. 综上可知,当
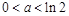 时, 函数
时, 函数 的最小值是
的最小值是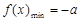 ;当
;当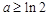 时,函数
时,函数 的最小值是
的最小值是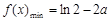 .
. 即
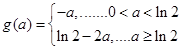 ………………14分
………………14分略

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
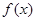 在
在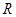 上可导,其导函数
上可导,其导函数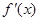 ,且函数
,且函数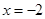 处取得极小值,则函数
处取得极小值,则函数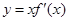 的图象可能是
的图象可能是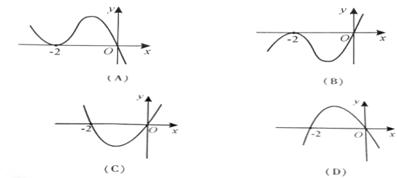
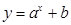 的图象如右图,则函数
的图象如右图,则函数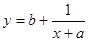 的图象为 ( )
的图象为 ( )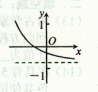

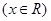 满足
满足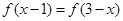 ,且方程
,且方程 的两个根
的两个根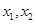 满足
满足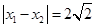 .
.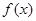 解析式;
解析式;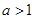 ,函数
,函数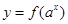 在
在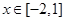 上的最小值为
上的最小值为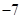 ,求
,求 的值.
的值.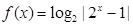 的图象大致是
的图象大致是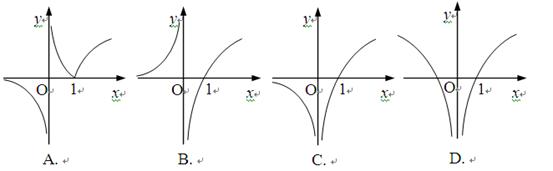
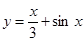 的图象大致是
的图象大致是
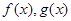 的图像分别如图1、2所示.函数
的图像分别如图1、2所示.函数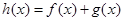 . 则以下有关函数
. 则以下有关函数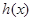 的性质中,错误的是(▲)
的性质中,错误的是(▲) 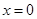 处没有意义;
处没有意义;

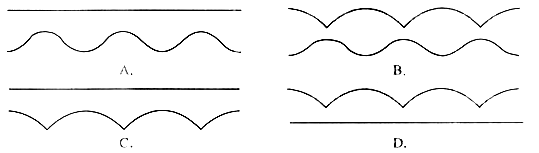
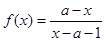 图像的对称中心是(3,-1),则实数
图像的对称中心是(3,-1),则实数 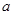 等于 .
等于 .