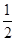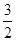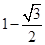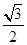题目内容
已知函数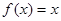 ,函数
,函数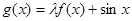 是区间
是区间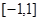 上的减函数.
上的减函数.
(1)求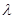 的最大值;
的最大值;
(2)若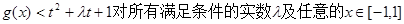 恒成立,求
恒成立,求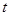 的取值范围;
的取值范围;
(3)讨论关于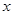 的方程
的方程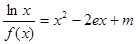 的根的个数.
的根的个数.
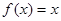 ,函数
,函数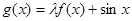 是区间
是区间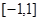 上的减函数.
上的减函数.(1)求
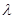 的最大值;
的最大值;(2)若
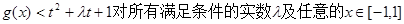 恒成立,求
恒成立,求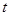 的取值范围;
的取值范围;(3)讨论关于
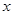 的方程
的方程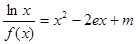 的根的个数.
的根的个数.(1)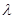 的最大值为
的最大值为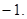 (2)
(2)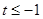 .(3)当
.(3)当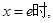
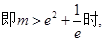 方程无解;
方程无解;
当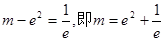 时,方程有一个根;当
时,方程有一个根;当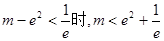 时,方程有两个根.
时,方程有两个根.
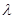 的最大值为
的最大值为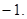 (2)
(2)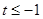 .(3)当
.(3)当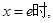
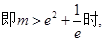 方程无解;
方程无解;当
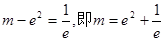 时,方程有一个根;当
时,方程有一个根;当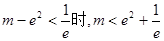 时,方程有两个根.
时,方程有两个根.试题分析:(1)由题意由于
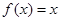 ,所以函数
,所以函数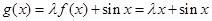 ,又因为该函数是在区间
,又因为该函数是在区间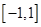 上的减函数,所以可以得到
上的减函数,所以可以得到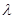 的范围;
的范围;(2)由对所有满足条件的实数及对任意
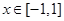 ,
,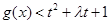 在
在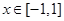 上恒成立
上恒成立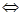
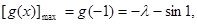 解出即可;
解出即可;(3)利用方程与函数的关系可以构造成两函数图形的交点个数加以分析求解.
试题解析:(1)
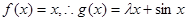 ,
,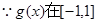 上单调递减,
上单调递减,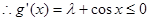
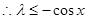 在[-1,1]上恒成立,
在[-1,1]上恒成立,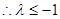 ,故
,故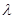 的最大值为
的最大值为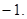
(2)由题意
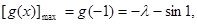
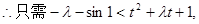
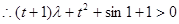 (其中
(其中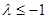 ),恒成立,
),恒成立,令
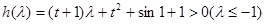 ,
,若
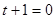 ,则有
,则有 恒成立,
恒成立,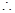
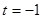
若
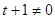 ,则
,则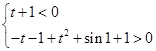 ,
,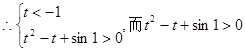 恒成立,
恒成立,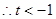
综上,
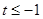
(3)由
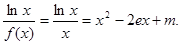
令
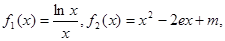
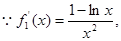
当
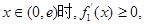
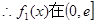 上为增函数;
上为增函数;当
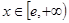 时,
时,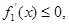
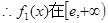 为减函数;
为减函数;当
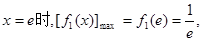 而
而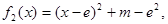
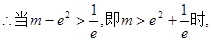 方程无解;
方程无解;当
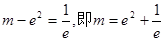 时,方程有一个根;
时,方程有一个根;当
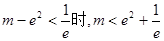 时,方程有两个根.
时,方程有两个根.
练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
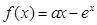
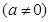 .
.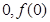 )处的切线方程;
)处的切线方程; 使得
使得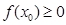 ,求
,求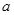 的取值范围.
的取值范围.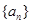 的前
的前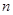 项和为
项和为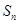 ,对一切正整数
,对一切正整数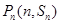 都在函数
都在函数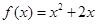 的图像上,且过点
的图像上,且过点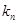 .
.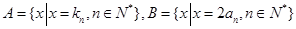 ,等差数列
,等差数列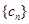 的任一项
的任一项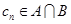 ,其中
,其中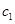 是
是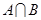 中所有元素的最小数,
中所有元素的最小数,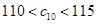 ,求
,求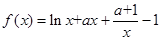 .
.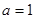 时,求曲线
时,求曲线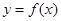 在点
在点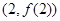 处的切线方程;
处的切线方程;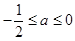 时,讨论
时,讨论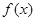 的单调性.
的单调性.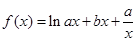 (
(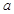 、
、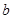 为常数),在
为常数),在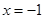 时取得极值.
时取得极值.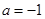 时,关于
时,关于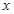 的方程
的方程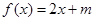 有两个不相等的实数根,求实数
有两个不相等的实数根,求实数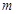 的取值范围;
的取值范围;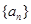 满足
满足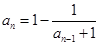 (
(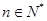 且
且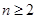 ),
), ,数列
,数列 项和为
项和为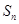 ,
,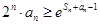 (
(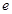 是自然对数的底).
是自然对数的底).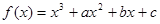 ,在定义域
,在定义域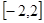 上表示的曲线过原点,且在
上表示的曲线过原点,且在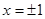 处的切线斜率均为
处的切线斜率均为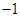 .有以下命题:
.有以下命题: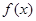 是奇函数;②若
是奇函数;②若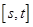 内递减,则
内递减,则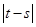 的最大值为4;③
的最大值为4;③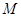 ,最小值为
,最小值为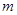 ,则
,则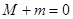 ; ④若对
; ④若对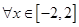 ,
,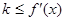 恒成立,则
恒成立,则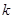 的最大值为2.其中正确命题的序号为
的最大值为2.其中正确命题的序号为 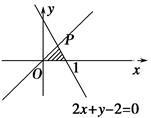
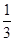
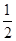
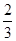
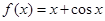 ,则
,则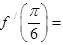 ( )
( )