题目内容
在等差数列 中,中若
中,中若 ,
, 为前
为前 项之和,且
项之和,且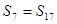 ,则
,则 为最小时的
为最小时的 的值为 .
的值为 .
12.
解析试题分析:从题目要求看,这个数列是递增的数列,前面若干项为负.接着可能有一项为零,再接着全为正,那么我们只要看哪一项为0,或者哪两项(相邻)异号,即能得出结论,由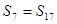 ,知
,知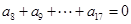 ,根据等差数列的性质,
,根据等差数列的性质,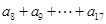 中
中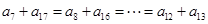 ,因此
,因此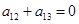 ,从而
,从而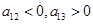 ,故所求
,故所求 为12.
为12.
考点:等差数列的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
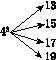
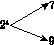
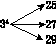
如图,对大于或等于2的自然数m的n次幂进行如下方式的“分裂”:
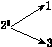 | 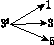 | 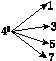 |
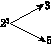 | 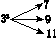 |  |
 |  |  |
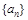 中,
中,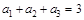 ,
, ,则该数列前20项的和为____.
,则该数列前20项的和为____.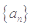 的前
的前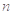 项和为
项和为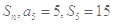 ,则数列
,则数列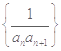 的前100项和为
的前100项和为 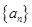 中,
中,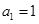 ,
,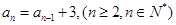 ,则
,则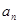 =___________.
=___________.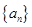 中,
中,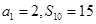 ,记
,记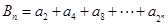 ,则当
,则当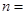 ____时,
____时,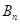 取得最大值.
取得最大值.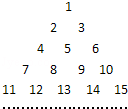
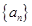 中,
中,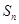 为其前n项和,若
为其前n项和,若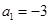 ,
,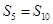 ,则当
,则当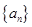 是等差数列,
是等差数列,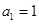 ,公差
,公差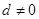 ,
,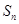 为其前
为其前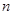 项和,若
项和,若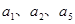 成等比数列,则
成等比数列,则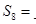 .
.